基于土地资源配置的房地产商合作博弈分析
- 加强房地产企业的财务管理
- 呼和浩特市房地产行业现状、主要问题和发展趋势
- 征地拆迁中的各方利益博弈和法律秩序的重建
- 浅议农村房屋拆迁补偿制度
- 妥善解决征地拆迁范围内房地产权问题
- 桂西北中心城区建设征地拆迁工作总结
- 城市建设征地拆迁中的职务犯罪分析
- 秦直道遗址的开发与保护研究
- 河南国网宝泉抽水蓄能电站投资计划管理实践
- 使用加气混凝土砌块做为保温墙体的节能分析
内容提示:基于土地资源配置,用博弈论的方法分析了房地产开发商之间是否应该进行合作。通过合作与不合作的对比,得出开发商之间合作不仅能提高二者的利润,而且由于土地资源的合理利用还能降低房价。
0 引言
房地产业经过 20 年的发展已成为我国的支柱产业,由于房地产投资超额利润的影响,有越来越多的有实力的公司转轨进入房地产领域,因此加剧了房地产开发商之间的竞争。由于竞争的激烈,开发商之间也上演了类似彩电行业的价格竞争,某些开发商建议在开发商之间形成联盟,面对这一情况有赞成者,也有批评者。批评者主要是认为联盟容易形成价格垄断,从而不利于行业的发展,对购房消费者不利。北京的土地出让价格是全国最高的,从而房价也是全国最高的,这主要是各开发商之间对土地资源的掠夺造成的,据某媒体报道,北京市在未来 30 年内已经几乎没有土地可出让了。为了房地产的健康发展,我认为目前主要面临的问题是如何合理利用土地资源,稳定房地产商品的价格,避免房地产投资的泡沫,扩大市场需求,以保证房地产业的可持续发展。(参考《建筑中文网》)
由于房地产商品的区域性,房地产的竞争主要是同一区域内(以下简称同一市场)的竞争,而房地产商品的价格是由同一市场的开发总量和消费者的需求决定的,一个开发商的受益必然要受到其他开发商开发量的影响。如果每个开发商都按照目前市场情况和自身的资源来规划开发规模,很可能导致部分商品房市场饱和而使开发商蒙受损失,或部分商品房市场价格过高,损害消费者的利益。因此,在房地产投资决策中自我式的决策,可能达不到预期的效果。
为了追求房地产投资的最佳效益,开发商应在有限资源下合理规划住房的开发结构与价格,从而获得最大利润。我们知道不同的开发商所具有的优势各不相同,为了各开发商之间优势互补,共同得利,合作是一种有效的手段。通过不合作向合作的转变,开发商由被动地适应市场转变为主动地适应市场,从而提高开发商和整个市场的效益。房地产开发过程是一种资源的投入过程,对这一过程需要大量的资金,需要各种专业人才,需要大量的信息,特别还需要土地资源。房地产开发商之间的竞争也是资源的竞争,是资源合理配置的竞争。
本文主要是研究同一市场上拥有土地资源的开发商之间的博弈,在分析中重点是关于土地资源的配置,主要是建立产量博弈模型,借以对合作与不合作的博弈结果进行比较。
1 土地资源最佳配置的博弈问题描述
目前很多大的开发商都进行了大量的土地储备,而目前很多开发商对项目进行分析时多依赖于自己对市场的预测而进行决策。由于房地产商品供给的滞后性,当某一开发商决策时,不了解其他开发商的意图,因此这种博弈可视为静态博弈。为了分析的要求,下面分别建立了不合作与合作 2 种模型。
设同一市场上的开发商有 n 家,即博弈的参与人集合为 N={1,2,3,…,n},i∈N 表示第 i 个参与人;第i 个参与人所拥有的土地面积为 Si,即土地资源占有可记为:S={S1,S2,…,Sn}。
每个参与人的战略空间是选择进行开发的商品房类型,如高档商品房、普通商品房等,设目前可供开发的商品房类型有 m 种,其战略空间为 j∈M,M={1,2,…,m},Sij 表示第 i 个参与人用于开发第 j类型商品房的土地面积。
每个参与人的支付函数设为利润,则第 i 个开发商开发第 j 种商品房的利润为 Eij,i=1,2,…,n; j=1,2,…,m。
在同一市场上同一类型的住房差异不大,可认为是同值的,又假定信息充分畅通,所以,对同一类型的住房价格相同,其大小由实际需要和总供给量决定,这样有
Ei j =(Pj-Cij)Sij qij
式中,Pj—— 第 j 种商品房的价格;Cij—— 第 i 个开发商开发第 j 种商品房的开发成本;Sij—— 第 i 个开发商开发第 j 种商品房的用地面积;qij—— 第 i 个开发商开发第 j 种商品房的允许建筑容积率。
在以上 4 个变量中,容积率 qij 和开发成本 Cij 一般是基本确定的,开发商 i 可以控制的变量是开发第j 种商品房的用地面积 Sij;销售第 j 种商品房的价格 Pj 由市场的总开发量 Qj 决定,有:
Pj=aj-bj Qj,
其中,aj,bj 为常数, Q j =∑Sij qij
因此,第 i 个开发商的利润为
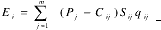
显然,这个决策问题与一般的决策问题有 2 点本质上的区别:一是多个开发商分别对自己所掌握的决策变量有自主决策权。二是每个决策者的多个目标不但取决于自身决策变量的选定,而且受到其他决策者所选定的决策变量的影响。
(1)若开发商之间不合作,即在同一市场上各自按自己的利润最大化选择其不同开发类型的土地面积。假设开发商没有资金的压力,即资金可以充分满足开发的需要,则决策问题为
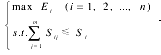
(2)若开发商之间合作,即在同一市场上按共同利益最大化原则确定各自的开发用地面积。设合作者之间制定的第 j 种房地产的最低价为 Pjd,最高价格为 Pjg,则决策问题为:
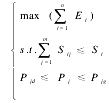
2 合作与不合作的比较分析
为了简化问题,只考虑同一市场上 2 个开发商的非零和博弈。
根据前面的分析,参与人集合 N={1,2},设 2 个参与人分别拥有土地面积为 S1,S2,开发的品种有高档商品房和中低档商品房,m=2。第 1 个参与人在高档和中低档商品房分配面积分别为 S11,S12,满足S11+S12=S1;第 2 个参与人在高档和中低档商品房之间分配的面积分别为 S21,S22,满足 S21+S22=S2。
支付函数分别为 E1 和 E2,则
E1= f1(S11,S12)
E2= f2(S21,S22)
(1)当两个参与人不愿意合作时,问题的解就是 Nash 平衡解( S11* , S21* ),它满足
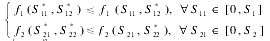
上式说明了决策双方任何一方独自偏离 Nash 平衡解,都只能对自己产生不利的结果。为求解上述问题,求解下式即可得 Nash 平衡解。
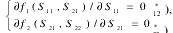
Nash 平衡解虽然保证了博弈双方任何一方独自偏离只能给偏离一方带来不利结果,但并没有保证双方的合作(同时偏离),也不会同时改进他们的结果,只是这种合作的可能性在非合作博弈中被排除掉了。
(2)如果 2 个参与人合作,即意味着可进行协商,并达成协议。协商博弈求解的思路是,如果博弈双方都能遵守一些共同的协商标准来选择对策的解,那么就可以在不存在一个真实仲裁人的情况下,按照上述的一个仲裁程序来求得协商博弈解。
对于上述描述的土地资源配置的问题,可以不合作博弈的 Nash 平衡解为冲突点,对应的效用为(d1, d2),在可达效用集中选一点 u =(u1,u2),使函数 f(u)=(u1- d1)(u2- d2)最大。如果博弈双方完全合作,则博弈目标为
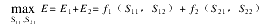
即求解: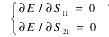
由上面分析可以看出,非合作博弈解都不是 Pareto 最优的,双方在这些解的基础上仍有改进的余地,但由于非合作假设的存在,使他们无法实现进一步的改进,而合作博弈通常都是 Pareto 最优的。
3 实例分析
假设在同一市场上有甲、乙 2 个开发商的土地面积 S1,S2 都为 1 万 m2,高档和中低档商品房的开发面积矩阵为
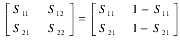
相应的容积率矩阵为 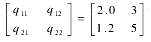
相应的单位成本(100 元/m2)矩阵为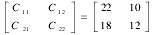
设高档和中低档商品房的反需求函数(单位:100 元/m2)分别为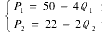
其中,Q1 = q 11 S 11 + q 12 S 12 ,Q = q21S 21 + q 22 S22
两个开发商的支付函数为 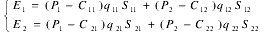
整理得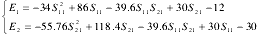
(1)Nash 平衡解。有: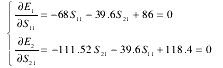
解方程组得 S11=0.814 9,S21=0.772 3
整理得 
从计算结果看出,虽然开发商拥有相同的土地资源,但由于容积率和成本的差异,其受益也不同。如果开发土地面积为 1 万 m2,则甲、乙开发商的盈利分别为 3 576 万元和 2 824 万元,共盈利 6 400 万元
(2)合作解。当博弈双方合作时,可求二人合作博弈解,其支付函数 E 为 #16.16
解方程组得 S11=0.902 6, S21=0.689 7
则 
如果开发土地面积为 1 万 m2,则甲、乙开发商的盈利分别为 3 752 万元和 2 767 万元,共盈利 6 519万元,比不合作时多盈利 119 万元。如果开发商土地储备越多,其盈利也越多。从上面的计算结果可以看出,在合作后高档商品房销售价格略有上升,中低档商品房销售价格略有下降;甲开发商盈利增加,不是靠价格联盟抬高房价,而是通过各自的条件优势互补,调整土地开发结构而实现,乙开发商的盈利有所下降。
4 结束语
对 2 个开发商就土地资源配置进行了博弈分析,通过对合作与不合作的对比,得出如果开发商之间合作,不仅能提高总利润,而且由于土地资源的合理利用还能降低房价。这就避免了一些人的担心,认为联盟就一定是价格联盟。随着住房市场的发展,房地产开发商之间的竞争日益加剧,为了避免恶性竞争,提高土地资源等的配置效率,开发商之间应该进行合作,合众联盟。
原文网址:http://www.pipcn.com/research/200605/227.htm
也许您还喜欢阅读:
