请告诉我们您的知识需求以及对本站的评价与建议。
满意 不满意
Email:
神经网络在工程造价和主要工程量快速估算中的应用研究
栏目最新
- 加强房地产企业的财务管理
- 呼和浩特市房地产行业现状、主要问题和发展趋势
- 征地拆迁中的各方利益博弈和法律秩序的重建
- 浅议农村房屋拆迁补偿制度
- 妥善解决征地拆迁范围内房地产权问题
- 桂西北中心城区建设征地拆迁工作总结
- 城市建设征地拆迁中的职务犯罪分析
- 秦直道遗址的开发与保护研究
- 河南国网宝泉抽水蓄能电站投资计划管理实践
- 使用加气混凝土砌块做为保温墙体的节能分析
网站最新
内容提示：采用动量法和学习自适应调整策略改正的BP神经网络建立了工程造价和主要工程量估算数学模型。针对以往估算模型精度不高的原因，模型中增加了工程造价指数和工程硬、软件环境对工程造价的影响。采用matlab6.1计算软件，以深圳市已完典型工程资料为例，验证了该模型的正确性及实
引言
人工神经网络是近年来迅速发展起来的一门新兴学科，是人工智能科学的一个分支，它是由大量的简单处理单元通过广泛的连接而形成的复杂网络。在经历了两次研究热潮之后，人工神经网络已经得到迅猛发展。目前，这一理论已渗透到生物、电子、数学、物理和建设工程等学科，有着广泛的应用前景。建设工程造价是组成建筑物的各分项工程的价格总和，而各分项工程的价格则取决于其工程量的大小和单价的高低。以往工程造价的计算是由造价编制人员算出各分项工程量，分别乘以其单价。由于组成建筑物的分项工程数量多，工程量的计算非常繁琐，计算时间占造价计算总时间的90%以上，所以计算结果容易出现误差。这表明造价计算的重点和难点在于工程量的计算。很多造价工程师根据其经验和一些学者提出的快速估算方法(相似工程法、模糊估算法等)来估如果能找到一种相对更快速和更精确的主要工程量和工程造价的估算方法，对造价计算工作具有重要的现实意义:以数学模型估算出来的工程量和造价作为参考依据，来检验手工计算的工程量和造价是否准确，预防工程量索赔的发生，从而有效控制造价。我们知道，某一建筑物的工程造价和主要的工程量主要取决于其工程特征。也就是说，某个建筑物的工程特征与工程量或造价之间存在一定的映射关系：Mapping：T={ti | i=1, 2,3,…,n}时一>Y，其中t表示工程特征，Y表示工程量或工程造价[1]。由于人工神经网络具有“特征提取器”的功能，且与其他估算方法相比，人工神经网络估算方法具有速度快、准确性高、不具主观性等优点，许多学者已经把人工神经网络应用到建设工程造价估算上来，并取得了可喜的成绩。但大多数神经网络估算模型主要是针对工程造价的估算，工程量估算罕见，远远不能满足工程量清单计价的要求。实际上，随着工程清单计价于2003年7月1日在全国范围内展开，对主要工程量的快速估算已成为客观要求。（参考《建筑中文网》）
本文尝试用BP神经网络建立工程造价估算模型，模型中增加主要工程量的估算输出，以适应工程量清单计价的要求，有效预防由于工程量人工计算误差引起的不平衡报价索赔现象的发生。
为提高估算的精度，论文数学估算模型中考虑了工程造价指数和工程硬、软件环境对工程造价的影响。尽管以往工程造价估算模型采取了优选典型工程等提高估算精度的措施，但效果仍然不明显，其主要结论。
1模型的建立
1.1人工神经网络模型选取
神经网络模型多种多样，BP (Back Propagation)网络是应用最多的一种，它又称误差反向传播网络。BP网络结构是一种多层网络结构，由输入层、一层或多层隐层和输出层组成，各层之间采用全互连接，但同一层单元间不相互连接。理论已证明，三层BP网络可以逼近任何复杂的非线性函数，为此，本文采用三层BP网络模型建模，其结构如图1所示。原因是忽略了价格指数波动和各施工单位、监理人员的管理水平、技术力量等工程硬、软件环境的差异对工程造价的影响。文中最后分析比较了考虑与不考虑工程造价指数和工程硬、软件环境两种情况下工程造价估算模型的精度，并得出了前者估算精度更高的结论。
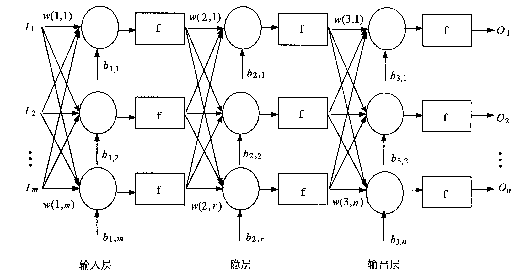
图1 BP网络结构图
Fig. 1 BP Network Frame
1.2模型参数的确定
1.2.1 BP网络模型结构参数的确定
网络结构参数的选取十分重要，直接影响网络的表达能力和收敛速度，这里选取隐层一层进行建模。输入层和输出层的神经元个数按实际需要确定，隐含层个数按柯尔莫哥洛夫定理取为2m +1(m为输入数据个数)。
1.2.2初时权值的选取
连接权系数和神经元阀值的初始值选取对网络模型是否达到最小，是否能够收敛以及训练的时间大小关系很大。本模型初始值采用随机函数((-1, 1)之间的随机数)在机上随机选取。
1.2.3节点函数的选取
选sigmoid函数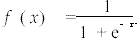 
为节点输出函数，其导数f’(x)=f(x)(1-f(x)),其优点是对于任何数据的输入都可以转化成（0，+1）之间的数。
1.3学习算法
BP算法的学习由四个过程组成:输入模式由输入层经中间层向输出层的“模式顺传播”过程;网络的希望输出与网络实际输出之差的误差信号由输出层经中间层向输入层修正连接权的“误差逆传播”过程;由“模式顺传播”与“误差逆传播”的反复交替进行的网络“记忆训练”过程;网络趋向收敛即网络的全局误差趋向极小值的“学习收敛”过程[2]。即“模式顺传播”→“误差逆传播”→“记忆训练”→“学习收敛”四个过程，这四个过程可以进一步合并为“正向传播”和“反向传播”两个过程。
算法描述如下[3]：
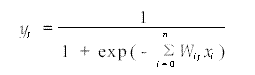
式中，二是结点/的输入结点个数xi是第i个输入结点的输出值,Wij是第i个输入结点到结点j的权值i=0时Wij和xi分别代表阈值和1。
(2)反射传播修改第K层结点的权值和阈值
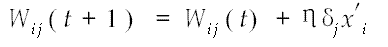
式中,Wij是K-1层结点i到K层结点j的连接权值和阈值，xi’是结点i的输出η是学习速率((0<η<1)。
当结点j是输出层时，取：
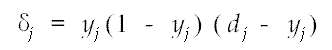
式中yj与dj分别是结点j的实际输出和期望值，否则取：
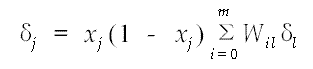
式中，xj是结点j的实际输出值，m是结点j的输出结点个数。
由于BP算法采用的是梯度下降法，即训练过程从某一起点沿着误差函数的斜面逐渐趋于最小点E→0，这就有可能会使整个网络模型陷于极小值点，同时BP算法学习速度较慢，为避免这些现象的发生，采用动量法和学习率自适应调整两种策略来抑制网络陷于局部极小和提高其训练速度。
动量法是在权值和阈值的调节公式中加入动量因子mc，其公式为：
其中：SSE为网络的输出误差和。
在学习过程中采用以下自适应学习速率的调整公式：
其中：SSE为网络的输出误差和。
2 实例分析
为了使问题简单化并提高模型的精度在进行建设工程造价估算时应区分工程类型。本例以框架结构多层住宅为例选取了11个典型工程（其中第11个工程用于检验)。在充分考虑了深圳市工程造价计价模式后本文选取了基础类型、基底标高、工程类别、墙体工程、门类型、门数量、窗类型、窗数量、楼地面、屋面工程、外墙装饰、内墙装饰、层数、层高、建筑面积、造价指数和工程硬、软件环境等17个影响工程造价和工程量的特征作为模型的输入，见表1。考虑到各个工程中门和窗数量差别很大为提高估算的精度我们把门数量和窗数量作为输入，其数量在工程施工图纸上很容易查得，不需作复杂的计算。对于其他文字性表达的工程特征需转变成数字后作为网络的输入，比如基础类型中条型基础取为1，独立基础取为2，满堂基础取为3，其他工程特征输入类推。
表1典型工程样本输入表
Table 1 Sample data input
以单方造价、每百平方米钢筋量、混凝土量、模板和砌块作为模型的输出，见表2数据。由于模型输出节点采用了sigmoid函数，表2中数据均转换成小数后作为模型的测试样本，比如单方造价以每万平方米为单位换算。
表2 典型工程样本输出和测试结果表
Table 2 Sample data output and test result
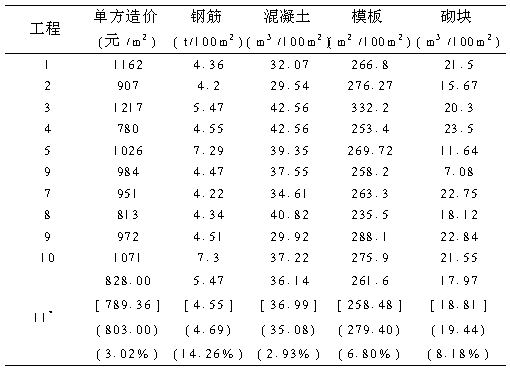
模型用m a tlab6. 1软件设计程序进行训练，误差设定为0. 0005，初始学习率取为0. 02。模型经21347次训练后达到预定的误差。测试的结果见表2圆括号中数字。方括号中数字为没有考虑造价指数及工程硬、软件环境的影响。
从测试结果看，考虑造价指数和工程硬、软件环境的数学模型比没有考虑的数学模型精度高，其工程造价估算为803. 00元/了，误差为3.02%，没有考虑造价指数的数学模型工程量的估算为789. 36元/了，误差为4.67。两数学模型在工程量上相差不大，考虑造价指数和工程硬、软件环境的数学模型的工程量最大误差为钢筋估算量，误差为14.26%,混凝土估算工程量误差为2.93，达到最小。
3 结论
通过实例可以得出以下结论：
(1)人工神经网络可以用于工程造价和主要工程量的快速估算。工程造价估算非常准确，而工程量估算误差相对较大(如钢筋估算误差为14.26%)，其主要原因是由不同设计人员设计带来的一些“噪声”(如钢筋的配筋率不一样)。
(2)造价指数和工程硬、软件环境是影响工程造价不可或缺的因素，考虑造价指数和工程硬、软件环境影响的数学模型比不考虑的数学模型估算工程造价的精度更高。
(3)可以采用本数学模型得出的数据作为同类工程的工程造价和主要工程量验证计算的参考依据，达到预防由于工程量计算误差引起的不平衡报价索赔的目的，从而有效控制工程造价。
原文网址：http://www.pipcn.com/research/200601/8.htm
也许您还喜欢阅读：