相变蓄热球体堆积床传热模型及热性能分析
- 低碳节能建筑设计的相关问题及解决方法
- 江苏建筑职业技术学院图书馆设计文化理念
- 四川雅安名山县涌泉村抗震小学的设计理念
- 四川汶川5.12大地震的启示
- 汶川大地震震中纪念馆的创作思考
- 洛阳洛南新区雅安新城结构设计
- 绿色居住建筑的节地设计
- 广州珠江新城海心沙地下空间建筑设计方案
- 黔东南地区郎德苗寨民居的热适应性
- 西气东输工程中长输管道站场建筑模块化设计与应用
内容提示:康艳兵 张寅平 江亿 朱颖心 简介 为提高普适性和预测性,建立了相变蓄热球体堆积床热性能的传热模型,可以对系统多种热性能参数进行计算分析。经验证明模型结果与实验结果较吻合。表明该模型对相变蓄热球体堆积床的结构设计、性能模拟及运行管理可提供理论指导。
康艳兵 张寅平 江亿 朱颖心
简介: 为提高普适性和预测性,建立了相变蓄热球体堆积床热性能的传热模型,可以对系统多种热性能参数进行计算分析。经验证明模型结果与实验结果较吻合。表明该模型对相变蓄热球体堆积床的结构设计、性能模拟及运行管理可提供理论指导。(参考《建筑中文网》)
关键字:蓄热 相变材料 传热 蓄冰 球体堆积床
近年来,随着人们节能和环保意识的不断增强,相变贮能系统应用日益广泛,在太阳能利用、区域供热和供冷(DHC)、建筑节能系统、蓄冷空调系统和一些余热回收系统中已经获得应用或正在引起研究者的关注[1,2]。
相变蓄热球体堆积床是相变贮能系统的一种常用结构形式,它具有单位体积的传热面积大、结构简单等优点。国内外学者对其储、传热特性进行了大量研究[3~8],但令人不能完全满意的是一些方法过于简化[5,6],难以全面反映系统热性能特征,一些方法仅对冰蓄冷情况进行了分析,有些参数需依靠实验确定,普适性和预测性不强。鉴于此,提出相变蓄热球体堆积床的传热模型,力求具有较宽的适用面(不局限于某一种工质和工况),较全面地反映系统的储、传热性能。文中模型既能模拟计算相变传热速率、流体出口温度、蓄热量等易测参数,也可求解沿轴向的相变界面及流体温度分布、系统的有效传热系数、有效传热面积、相变材料发生相变的比例等难测参数随时间的变化规律。模型计算结果与文献[8]实验结果较吻合。作为算例,利用文中模型对该实验台其它热性能参数进行了模拟分析。该模型对相变蓄热球体堆积床的结构优化设计和性能模拟分析有一定帮助。
1 传热模型相变蓄热球体堆积床的结构如图1(a) 所示。
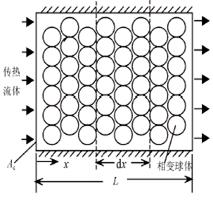
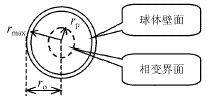
(a) 相变球体堆积床示意图 b) 单元相变球体结构参数
图1 相变蓄热球体堆积床结构图
为了突出问题本质并使问题合理简化,作如下假设:
1) 相变传热过程的斯蒂芬数Ste<<1,即在相变过程中可忽略显热的影响;
2) 对融化问题,忽略相变材料液相自然对流;
3) 传热流体流程长度远大于球径,即L>>2r0;
4) 球体内固相和液相无密度差,各相内物性均一;
5) 掠过单元球体外表面的流体温度及对流换热系数的不均匀性可忽略。
由假设4)和5)可知,单元球体凝固与融化过程相变界面呈同心球形状,如图1(b)所示。
1.1 传热模型
对图1(a)所示的微元体,传热流体和相变球体应满足的能量平衡方程为
对相变球体:
 (1)
(1)
对传热流体:
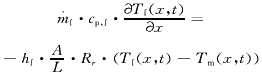 (2)
(2)
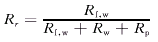 (3)
(3)
其中,下角标p,f,w分别代表相变材料、流体和球壳。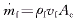 为流体流量,
为流体流量,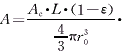 4πr30为堆积床中相变球体的总传热面积,Rf,w=
4πr30为堆积床中相变球体的总传热面积,Rf,w=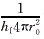 为流体和球体壁面间的对流换热热阻,Rw=
为流体和球体壁面间的对流换热热阻,Rw=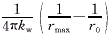 为球壳导热热阻,
为球壳导热热阻,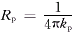
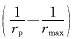 为相变层导热热阻。 Ac和ε分别为堆积床的横截面积和孔隙率。
为相变层导热热阻。 Ac和ε分别为堆积床的横截面积和孔隙率。
初始条件:rp(x,t=0)=rp,0 (x),Tf(x,t=0)=Tf,i;
边界条件:Tf(x=0,t)=Tf,in (t)。
1.2 量纲为1化
为了更本质地刻画该类相变换热器的共性特征,拓宽模型的适用范围,对涉及参数及方程进行了量纲为1化:
令
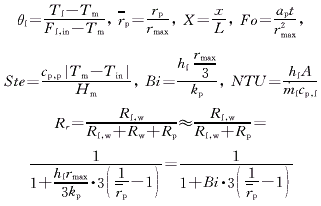
由式(1)和式(2),得
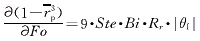 (4)
(4)
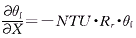 (5)
(5)
初始条件:
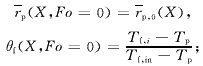
边界条件:θf(X=0,Fo)=1.
解方程(4)和(5),得
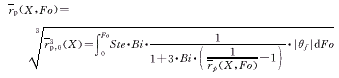 (6)
(6)
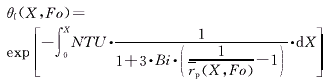 (7)
(7)
对给定的X、Fo,根据式(6)、(7)进行迭代求解可求出θf(X,Fo)和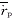 (X,Fo)。某一位置某一时刻的迭代初值为θ*f(X,Foi)=θf(X,Foi-1)和
(X,Fo)。某一位置某一时刻的迭代初值为θ*f(X,Foi)=θf(X,Foi-1)和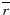 *p(X,Foi)=
*p(X,Foi)=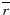 p(X,Foi-1),即取同一位置上某一时刻值作为迭代初值。
p(X,Foi-1),即取同一位置上某一时刻值作为迭代初值。
当某一轴向截面上的球体全部发生相变,即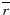 p(X,Fo)=0时,记此时该截面距进口处的无量纲距离为Xin(Fo) ,见图2。此后的相变传热过程仅发生在X>Xin部分,而X≤Xin部分仅有显热传热,因为Ste<<1,即相变材料的显热远小于其潜热,所以可忽略此部分传热,于是式(7)的积分下限应取Xin。这说明堆积床相变传热过程中有效传热面积会逐渐减小,它占总传热面积的比例为
p(X,Fo)=0时,记此时该截面距进口处的无量纲距离为Xin(Fo) ,见图2。此后的相变传热过程仅发生在X>Xin部分,而X≤Xin部分仅有显热传热,因为Ste<<1,即相变材料的显热远小于其潜热,所以可忽略此部分传热,于是式(7)的积分下限应取Xin。这说明堆积床相变传热过程中有效传热面积会逐渐减小,它占总传热面积的比例为
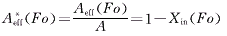 (8)
(8)
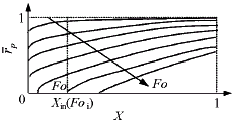
图2 相变界面随时间变化规律示意图
在有效传热面积上无量纲有效总传热系数,即有效总传热系数与对流换热系数之比为
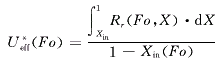 (9)
(9)
对于给定的系统,求出θf(X,Fo)和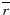 p(X,Fo)后,可以计算其逐时储、放热速率、逐时蓄热量和相变蓄热比,即蓄热量与最大蓄热量之比,其分别为:
p(X,Fo)后,可以计算其逐时储、放热速率、逐时蓄热量和相变蓄热比,即蓄热量与最大蓄热量之比,其分别为:
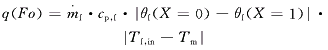 (10)
(10)
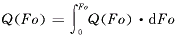 (11)
(11)
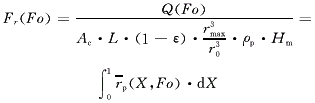 (12)
(12)
1.3 模型适用范围讨论
1) 应满足前文的5个假设。
2) 适用于入口处流体流量及温度随时间变化和局部对流换热系数不为常数的情况。因此可藉此模型分析变流量、变进口温度及需考虑进口段效应的情况。
3) 适用于计算初始时刻有残余固相或液相相变材料的情况。
4) 适用于相变传热过程中有效传热面积变化的情况。
5) 适用于相变材料固液相密度差较小及流体温度与相变材料融点相差不大的情况。
2 模型验证利用本实验室球形冰蓄冷装置[8],在蓄冷和放冷两种工况下,将本文模型计算的流体出口温度和逐时蓄热量与实验结果的进行了比较(见图3~6)。
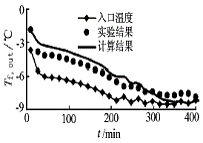
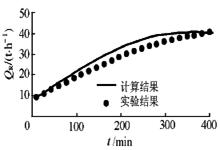
图3 流体出口温度比较(蓄冷工况) 图4 逐时蓄热量比较(蓄冷工况)
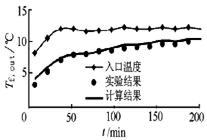
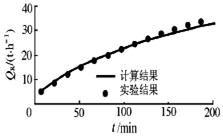
图5 流体出口温度比较(放冷工况) 图6 逐时蓄热量比较(放冷工况)
图3和图4表明,蓄冷初期流体出口温度的计算值比实验值偏高,而在后期偏低,逐时蓄冷量的计算值比实验值偏高。图5和图6表明,在放冷过程中,流体出口温度计算值比实验值略高,而逐时放冷量在初期基本一致,在后期计算值偏低。导致偏差的原因为:1)实际系统中流体流速的分布不完全均匀,且球体内充水不足; 2) 模型中按相变材料以同心圆方式发生相变,与实际情况不完全相符; 3) 模型中未考虑球内水的自然对流换热和固、液相密度差造成的接触传热问题; 4) 模型算法误差。但可看出,模型计算值与实验值差别不大,用此模型可预测系统的蓄、放冷性能。
3 蓄冰实验台其它热性能的分析球体堆积床的一些热性能参数,例如相变材料的相变比例、系统的有效传热系数、相变界面沿轴向的分布情况和流体温度分布随时间的变化规律对系统的运行管理及结构优化设计有一定帮助。有些参数,如相变材料的相变比例在球体堆积床中很难测定。藉此模型可以对上述参数进行动态模拟,从而对系统性能进行分析,以提供系统设计及运行管理的依据。为说明模型在这方面的应用,作为算例,对前文所述的实验台放冷工况的有关热性能进行了进一步的模拟分析,见图7~11。
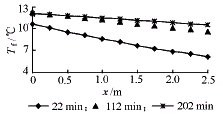
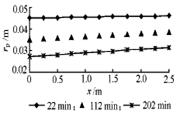
图7 不同时刻的流体温度分布 图8 不同时刻的相变界面分布
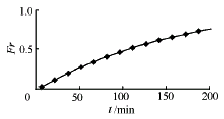
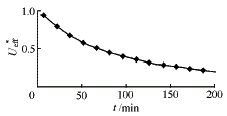
图9 相变比例随时间的变化情况 图10 无量纲总传热系数随时间的变化情况
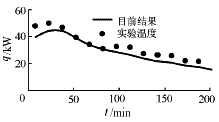
图11 相变传热速率随时间的变化情况
图7~10分别描述了放冷过程中流体温度分布、相变界面、相变材料中发生相变的质量比和无量纲总传热系数随时间的变化趋势。图11显示了传热速率随时间变化的实验及计算结果。由图可见,模拟结果基本反映了实际变化规律,数值上也较吻合。
由上述分析及图7~11可看出:
1) Fr和Ueff是系统设计和运行管理的重要参数,但实际系统中难以监测。藉此模型可对系统性能进行分析,从而为系统设计和运行管理提供帮助。
2) 对实际系统,往往只对很有限的典型运行工况进行性能实验,所得实验结果难以外推。藉此模型,可利用有限的实验结果,预测系统在其它工况下的热性能。
4 结语1) 建立了分析相变蓄热球体堆积床热性能的传热模型,它对流体入口流量、温度随时间变化的情况和需考虑进口段效应的情况均适用,并能计算多种相变传热性能参数,对系统性能进行分析,从而为系统设计和运行管理提供帮助。
2) 通过与文[8]所述的蓄冰实验台的实验结果比较,验证了模型的正确性。
3) 藉此模型,可分析各种因素对系统热性能的影响规律,为系统设计提供帮助。
4) 球体内液相材料的自然对流及接触传热效应较强的相变过程有待进一步分析。
参考文献:[1]Beckman G,Gilli P V.Thermal energy storage [A].Wien,Austria: Springer-Verlag,1984.
[2]张寅平,胡汉平,孔祥冬,等.相变贮能—理论和应用 [M].合肥:中国科技大学出版社,1996.
原文网址:http://www.pipcn.com/research/200612/8750.htm
也许您还喜欢阅读:
