请告诉我们您的知识需求以及对本站的评价与建议。
满意 不满意
Email:
钢框架高级分析中的改进塑性铰法
栏目最新
- 低碳节能建筑设计的相关问题及解决方法
- 江苏建筑职业技术学院图书馆设计文化理念
- 四川雅安名山县涌泉村抗震小学的设计理念
- 四川汶川5.12大地震的启示
- 汶川大地震震中纪念馆的创作思考
- 洛阳洛南新区雅安新城结构设计
- 绿色居住建筑的节地设计
- 广州珠江新城海心沙地下空间建筑设计方案
- 黔东南地区郎德苗寨民居的热适应性
- 西气东输工程中长输管道站场建筑模块化设计与应用
网站最新
内容提示：本文回顾了钢框架高级分析的几种方法和研究现状，重点介绍了改进塑性铰法对钢框架的分析和设计，并讨论了当前高级分析及改进塑性铰法存在的困难，为高级分析方法的进一步发展提供参考。
1. 简 介
钢结构高级分析[1-2]（亦称为整体分析[3]）是指通过精确的非线性分析，完善的考虑结构的二阶效应及其它非线性因素的影响，通过一次性分析，完成目前先进行内力分析再进行结构验算的两阶段设计所做的工作。高级分析方法同时考虑影响钢结构及其构件的极限状态强度和稳定的关键因素。由于非线性效应是在结构分析中直接考虑的，所以用高级分析方法设计钢框架时，通常不需要进行当前设计规范条文中强制性的单个构件验算。这种综合性的设计和分析方法从本质上保证了对设计过程的简化，使工程设计人员能够了解要设计的结构在不同荷载水平下的行为和其破坏模式。澳大利亚首先在其1990年版本钢结构规范AS4100中允许将高级分析方法作为一种可选方法，以简化不发生局部屈曲和侧向屈曲的钢框架的设计[4]。欧洲标准EC3-1991也做了相应的规定[5]。（参考《建筑中文网》）
空间钢框架的二阶非线性分析有多种方法[6,3,7-8]，这些方法大致可以分为：（1）塑性区法(plastic zone method) [9,28-29,31]。塑性区高级分析方法将构件截面划分成若干有限面积分区，截面的切线刚度就由这些面积分区的弹性特性形成，截面的抗力和弯矩也由分区面积的抗力效应累加形成，利用牛顿-拉普森系列迭代法使不平衡的内力和外力重分配。文献[10]介绍了塑性区法求解钢框架极限荷载的过程。很多学者认为塑性区法是精确的。但是由于划分的单元数量特别多，造成结构的整体刚度矩阵十分庞大，在计算机计算分析过程中会导致较大的截断误差，迭代过程中更容易发散，耗时较长。目前许多大型非线性分析软件采用了塑性区法，或者包括塑性区法的多种混合方法。这些软件包括ABAQUS、ANSYS、MARC等通用的商业软件。随着个人计算机性能的快速提高，用这种方法进行大型结构的分析和辅助设计是可能的。（2）准塑性铰法(quasi plastic hinge method)[11]。准塑性铰法是介于塑性区法和塑性铰法之间的混合方法，该方法利用柔性系数考虑塑性的扩展，使用简化的残余应力模式，全截面塑性用塑性区法标定。该方法很难进一步发展用于空间结构分析。（3）塑性铰法(plastic hinge method，or concentrated plasticity method)及以塑性铰概念为基础的改进方法。塑性铰高级分析方法将构件的屈服集中到几个截面上，用弹簧模拟塑性铰形成截面的切线刚度。这样塑性铰法避免了将一个截面划分成多个小的面积分区，多数构件只需划分成一两个单元，并且保持了较高的精度，这就大大减小了结构刚度矩阵的大小，简化了计算机分析过程，提高了效率。
尽管实际上所有的框架都是三维的空间结构，但是有些结构可作为二维平面框架分析，比如不允许局部屈曲和侧向屈曲的框架，在一阶弯矩、轴向力和面内失稳造成的二阶效应综合作用下，由于屈服过度而破坏。高级分析方法正是从受二维荷载的二维框架分析开始发展起来的，而后在此基础上进一步研究了局部屈曲和侧向屈曲不太重要的三维框架，比如管结构。表1列出了高级分析针对不同类型的框架几种分析方法的特点[8]：
| 框架类型 | 荷载类型 | 失效形式 | 失效原因 | 特别情形 |
| 平面框架 | 面内受力 | 平面内 | 屈服 | 平面内屈曲 |
| 平面框架 | 面内受力 | 平面内 | 局部屈曲 | 局部屈曲后 |
| 平面框架 | 面内受力 | 出平面 | 侧向屈曲 | 屈服及翘曲 |
| 平面框架 | 空间受力 | 双向弯曲和扭转 | 屈服 | 扭转 |
| 平面框架 | 空间受力 | 双向弯曲和扭转 | 局部屈曲 | 局部屈曲后 |
| 空间框架 | 空间受力 | 双向弯曲和扭转 | 屈服 | 扭转 |
| 空间框架 | 空间受力 | 双向弯曲和扭转 | 局部屈曲 | 局部屈曲后 |
表1 高级分析中的几种方法
目前，二维框架的平面内分析相对较多，考虑其侧向屈曲的研究并不多。真正针对三维框架空间受力情形的严格分析非常少。
2. 塑性铰法及其改进 塑性铰法最初发展起来的是弹塑性铰分析法[12-13]。该方法一般假定构件不发生局部屈曲，即限定构件采用紧凑型截面（compact section）。允许单元端部形成零长度的塑性铰，单元的其他部分则保持完全弹性。这一方法从一定程度上考虑了非弹性，但不考虑屈服在塑性铰形成截面上以及在两铰之间的扩展，两铰之间残余应力的影响不能考虑。这种简单的方法用稳定函数模拟几何非线性。对于主要发生弹性屈曲的细长构件，弹塑性铰法与塑性区法计算结果符合很好；然而对于发生较大屈服并伴随塑性扩展的粗短构件，由于忽略了屈服沿构件的扩展，不能考虑构件因渐进屈服过程造成的刚度削弱，用该方法预测承载能力误差较大。文献[3]指出，弹塑性铰法得到的计算结果对于细长柱内力较小的刚架与塑性区法较接近，但是一般多层多跨刚架的承载力均偏高，有的刚架偏高的幅度很大。
一些学者致力于研究基于塑性铰概念的改进方法—改进塑性铰法。Orbison、Prakash和Powell、Chen、Liew和Tang、Kim等、Wongkaew，以及其他研究者，利用塑性铰法或者改进塑性铰法作了钢框架二阶非线性分析的研究。Orbison使用弹塑性铰分析方法，材料非线性用切线模量考虑，几何非线性用几何刚度矩阵处理。该方法不考虑剪切变形，对仅承受轴向力的短构件误差较大。Prakash和Powell改进了塑性铰法并推出了DRAIN-3DX分析软件，材料的非线性用截面纤维的应力-应变关系体现，由轴向力引起的几何非线性用几何刚度矩阵体现，但是由轴向力和弯曲相关作用引起的几何非线性不予考虑。该方法高估承受大轴向力构件的强度和刚度。Liew和Tang使用的是改进塑性铰法，残余应力用传统的梁-柱有限元模型考虑，材料非线性以计入描述材料屈服面-边界面（yield and bounding surfaces）的非弹性参数的方式考虑。该方法对仅承受轴向力的短构件低估其屈服强度最大达7%。Chen等所用的改进塑性铰法用稳定函数考虑几何二阶效应，CRC切线模量考虑残余应力，同时也提出了处理几何缺陷的具体方法[7]。这种方法考虑的因素较为全面。总的来看， Chen 、Liew和Kim等发展的改进塑性铰法可以考虑以下两种刚度退化：1）塑性铰形成截面的刚度退化。2）两塑性铰之间构件的刚度退化。这种方法和弹塑性铰法一样简单有效，同时保持了对结构体系及其构件承载能力和稳定性计算的较高精度。
经过多年的研究，改进塑性铰法在分析二维框架的平面内分析方面已比较成熟，开始向空间框架高级分析延伸。有研究者主张先利用现有塑性铰法进行平面内分析，再进行考虑残余应力和初始几何缺陷的基于非线性侧向屈曲分析的实用高级分析。这方面的例子见文献[14,15]。文献[14]用LRFD公式计算不同侧向支撑长度下的侧向扭转屈曲强度，如果无侧向支承的长度超过发生全截面（面内）屈服的极限长度，则用侧向（弹性或非弹性）扭转屈曲强度代替全截面屈服强度，代入考虑轴向力与弯矩相关作用的截面塑性强度公式（AISC-LRFD双线性相关公式）。文献[15]分别进行平面内分析和平面外屈曲分析，用“有效刚度法”综合考虑所有材料非线性、残余应力和几何缺陷对平面外屈曲的影响。对空间框架的分析见文献[7,16-17]。其使用的分析单元共有12个自由度（每个端部6个），忽略了翘曲约束的影响。
另外，对改进塑性铰法高级分析其他有关问题的研究也取得了进展。Chen、Liew、Kim、Yoshiaki Goto、N. Kishi等研究了钢框架的半刚性连接问题[18-23]，使得结构整体分析中可以考虑连接的半刚性及其剪切变形影响。Kim等又进一步研究了考虑局部屈曲效应、应变反转的方法以及有关弱轴弯曲的处理办法[24-26]。关于改进塑性铰法在抗震设计中的应用方法可参考文献[27]。
改进塑性铰法可以考虑二阶效应、材料非线性和几何缺陷等多种非线性因素的影响，利用计算机程序对钢框架进行整体分析，并且具有对计算机性能要求不高、计算省时同时又可以满足工程设计精度要求等优点，有可能取代当前各国规范普遍采用的基于单构件设计的方法，成为实用的二阶非线性钢框架设计方法。但是因为塑性铰法没有像塑性区法一样将截面分成面积分区，所以很难精确考虑局部屈曲和平面外屈曲特别是翘曲效应，对局部变形、翘曲与轴向力和弯矩间的相关作用、端部翘曲约束的模拟还比较困难。目前该方法一般不考虑屈曲前效应和屈曲后效应。
塑性区法用于结构分析较早，国内外的研究成果相对多一些。Vogel用塑性区法（塑性分配法）分析了紧凑型截面二维框架[28]，其结果被广泛用作检验框架分析精确程度的标准。Avery则分析了非紧凑型截面框架，给出了详细的壳单元分析模型[29]，并且做了大型试验检验其分析模型的精度[30]。Jiang等利用塑性区法进行三维钢框架非线性分析[31]，用塑性扩展模型模拟结构构件，考虑了残余应力、初始缺陷以及压力、弯曲和扭转的耦合效应，但限制局部屈曲，不能考虑侧向扭转屈曲。其所编制的计算机程序要达到塑性铰法程序相同的精度，需要将构件划分为7个单元，这也证实了塑性铰法的效率。此外，Yeong-B. Y和Kuo-S. R对框架体系的几何非线性分析进行了深入的分析，并首次提出了利用“广义位移法”求解非线性方程[32]。Buonopane等总结了高级分析设计的可靠度研究，考虑结构特性和荷载的随机性[33]。
国内的王孟鸿采用薄壁构件理论考虑了构件截面翘曲的影响，进行了各向同性损伤理论塑性区分布模型的弹、塑性区双重非线性分析，以及考虑局部屈曲、节点区变形和半刚性连接的三维空间钢结构非线性分析，并且在理论分析基础上编制了实用的三维空间钢结构的弹、塑性分析软件[34]，所做的工作目前是国内较为全面的。舒兴平等作了钢框架结构二阶弹塑性稳定极限承载力的试验研究和分析[35-36]，郭兵、顾正维、王新武等对刚框架的半刚性连接作了研究[37-39]。沈世钊教授、董石麟教授、张耀春教授、尹德钰教授对空间单层网壳结构的非线性行为进行了深入研究，他们的研究内容也是空间结构高级分析的重要组成部分[40-45]。国内其他研究者对刚框架及其构件非线性分析等问题作了研究[46-48]。
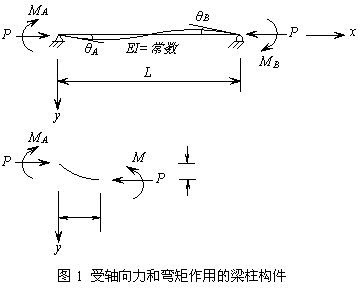
改进塑性铰法对各种非线性影响因素采用了简单实用的近似处理方法。鉴于Chen、Liew、Kim、Wongkaew等发展的改进塑性铰法在目前基于塑性铰概念的高级分析方法中考虑的问题较为全面，本文以这种方法为基础详细介绍改进塑性铰法的基本概念和技术。这里先介绍平面框架的平面内分析，再介绍平面外分析。
4.1 改进塑性铰法二维框架平面内分析
对二维框架的平面内分析，改进塑性铰法考虑二阶几何效应、与残余应力和弯曲相关的渐进屈服以及几何缺陷等非线性因素。具体解决方法如下面各小节所述：
4.1.1 稳定函数考虑几何二阶效应
Chen和Lui提出了简化的稳定函数，用以体现大位移情况下二阶几何效应。通常一个构件只需分成一个或两个单元。按照图1所示梁柱单元，该单元增量形式的力-位移关系可以用公式（1）表示为：
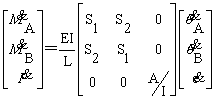（1）
这里，S1，S2＝稳定函数；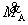
，
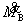＝增量形式端弯矩；
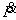＝增量形式轴向力；
，
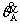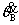＝增量形式连接转角；
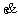增量形式轴向位移；A，I，L＝面积，初始惯性矩，梁柱单元长度；E＝弹性模量。稳定函数由下式定义：
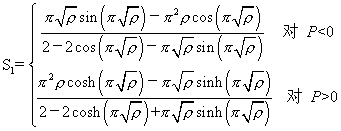（2）
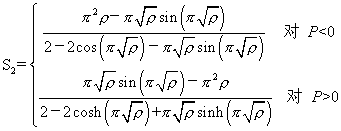（3）
这里ρ＝P／(π2EI／L2)，P以受拉为正。
当轴向力为零时公式（2）、（3）无解。为解决这一问题并避免轴向力变号时公式（2）、（3）不一致，Lui和Chen建议用幂级数展开式近似稳定函数。当构件中的轴向力在-2.0<ρ<2.0范围内时，可以用下面简化的表达式近似稳定函数：
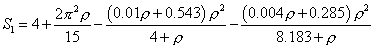（4）
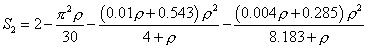（5）
在绝大多数实际应用中，公式（4）、（5）与精确表达式（2）、（3）符合得非常好(对ρ在-2.0<ρ<2.0范围外的情况，应当用公式（2）、（3）)。稳定函数法对每个构件只用一个单元，即可保证任意轴向力大小作用下单元刚度各项和求解的轴向力的精度。该公式应用的前提是所有构件都有足够的平面外支撑，以保证不发生平面外屈曲；构件截面均为紧凑型截面。
4.1.2 截面的塑性强度
根据AISI-LRFD双线性相关公式，截面的塑性强度可以用下式表达：
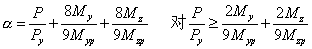（6）
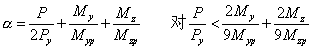（7）
这里P,M＝二阶轴向力和弯矩； Py＝压屈强度； Mp＝全截面塑性弯矩。
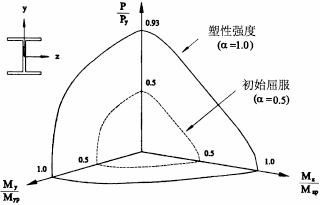
Orbison提出的截面塑性强度用下式表达：
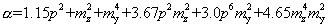（8）
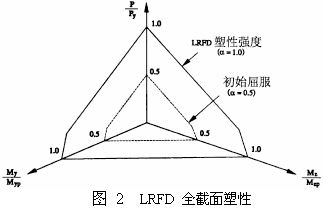
这里，p＝P/Py，mz＝Mz/Mzp(强轴)，my＝My/Myp(弱轴)，Py＝屈服荷载，Myp、Mzp分别是绕y轴和z轴的塑性弯矩。α是力状态参数，α＝0.5时开始屈服，α＝1.0达到全截面屈服。这两种截面的塑性公式见图2、图3所示：
这两种塑性强度公式可以用于空间框架结构。对于平面架，简化为以下两个公式：
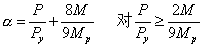（9）
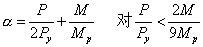（10）
这里P，M＝截面的二阶轴向力和弯矩；Mp＝全截面塑性弯矩。
4.1.3 CRC切线模量考虑残余应力
对塑性铰间承受轴向力的构件，用CRC（Column Research Council，美国柱研究局）切线模量考虑由于残余应力导致的沿构件长度渐进屈服。这里减小弹性模量的大小以代替减小初始惯性矩I的大小，以体现截面弹性核减小造成的刚度降低。刚度沿强轴和弱轴减小的速率是不同的，这里并未考虑，因为弱轴刚度的快速减退可以由富余的弱轴塑性强度补偿。Chen和Lui建议的Et表达为：
（11）
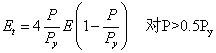（12）
4.1.4 抛物线函数考虑弯曲影响
切线模量模型适于受轴向力的构件，但对既承受轴向力又承受弯矩的情况，需要引入考虑弯曲塑性效应的塑性铰逐渐软化模型，用以体现塑性铰由弹性到刚度为零的过程。如果单元两端都在发展塑性铰，增量形式的力—位移关系可以表达为：
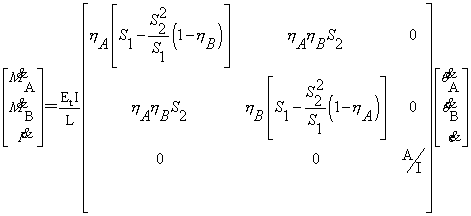（13）
ηA、ηB＝单元刚度参数，用以体现由弯曲引起的刚度的逐渐减小。单元端部的截面塑性状态由η在1和0之间变化来体现。η假定按照抛物线表达式变化：
（14）
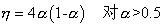（15）
这里α是力状态参数，由单元端部极限状态面得出。此外，还可以进一步修正单元刚度矩阵以便考虑剪切变形的影响[7]。
4.1.5 几何缺陷
通常有三种处理方法考虑制造或安装误差：明确缺陷模型法、等效节点荷载法、进一步减小切线模量法。
1)明确切线模型法
可以取规范规定的最大构件误差作为几何缺陷。比如美国AISI规范允许每层的垂直误差不超过Lc/500，可以采用Lc/500作为几何缺陷限值。无支撑框架可以考虑垂直误差几何缺陷，有支撑框架则不需考虑，因为垂直误差引起的P-∆效应可以由侧向支撑抵消。对有支撑框架，应当用构件的直线误差代替垂直误差作为几何缺陷。可以取规范规定的最大构件误差作为几何缺陷，比如， AISI建议对构件取其最大制造误差为Lc/1000。直线误差可以认为沿构件呈正弦波变化，在构件中央达到最大值Lc/1000，然而研究发现每个构件只用两个单元而构件中央有最大位移（缺陷）的模型已足以反映缺陷效应。
2)节点荷载法
框架的几何缺陷可以用等效的侧向节点荷载代替，用作用在框架一层上的重力荷载表达。建议用0.002∑Pu作为等效节点荷载，Pu是一层上的全部重力荷载。等效的侧向节点荷载作用在每一层的顶部。对有支撑框架，等效节点荷载应作用在柱的中间位置，大小取0.004∑Pu。这和几何缺陷Lc/1000相当。
3)进一步减小切线模量法
为考虑几何缺陷的影响，可以进一步减小切线刚度Et，也就是用减小切线刚度Et的办法体现由于几何缺陷造成的构件刚度逐渐退化。可以进一步减小CRC切线模量为：
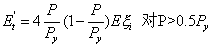（16）
（17）
这里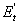
＝减小的Et；ξ'＝几何缺陷减小系数。
经大范围框架和柱子计算验证，减小系数取值0.85。这种方法比另外两种方法在设计中更为简便，既不用在单元模型中加入明确的几何缺陷，也不用另外施加等效节点荷载，并且不必考虑几何缺陷的方向，而在分析大型的有侧向支撑框架时确定最不利几何缺陷方向往往很困难。根据文献[3]的分析，等效节点荷载法和进一步减小切线刚度法的精度是令人满意的。
4.2 考虑平面外屈曲的方法
有关单个梁（受压）和梁柱（压弯）构件的侧向屈曲有很多研究成果，但对于框架结构体系中的侧向屈曲问题目前的研究还不多。在结构中构件的翘曲往往与构件间的相关作用有关。比如，对于相互垂直连接的工字形构件，一个构件的扭曲将导致另一构件的翼缘翘曲，而翘曲构件翼缘的双弯矩会影响前一构件的翼缘扭曲。此外，各种形式的连接其传递扭曲或翘曲的能力也各不相同。因此，针对结构体系考虑侧向屈曲是一个非常复杂的问题。
4.2.1 考虑平面外侧向屈曲的条件
钢框架建筑中，梁构件一般由楼板提供了足够的面外约束，能充分发展面内强度，而梁-柱（压弯）构件只在其端部有面外方向的约束，可能发生平面外弯曲或扭曲。根据参考文献[15]的研究，在面内荷载的作用下，无侧移（有侧向支撑）平面钢框架建筑中的柱构件通常由综合弯曲屈曲和扭转屈曲的平面外失效模式控制，有侧移（无侧向支撑）平面钢框架建筑中的柱构件也可能由平面外失稳控制。因此，对于钢框架建筑中的梁构件用平面内高级分析方法就可以了，对其柱构件则需进行平面外高级分析。
4.2.2 考虑平面外侧向屈曲的简化方法
严格来讲，二维框架由于其两个主平面的初始弯曲和初始扭转，实际上受双轴弯曲和扭转作用。但目前研究实用的双轴弯扭屈曲高级分析方法还很困难，充分考虑平面外弯扭屈曲失效模式的实用高级分析技术还不存在。于是，有研究者建议把分析简化为平面内和平面外两个独立的阶段，首先进行塑性铰法平面内高级分析，再进行平面外高级分析。一些国家的规范也要求分别进行平面内和平面外承载力验算。这种简化的方法使得当前可行的平面内分析方法在第一阶段可以保留使用，只需要研究平面外分析方法，而且平面内分析使用的结构形状及得到的弯矩和轴向力分配可以直接作为输入数据用于平面外分析。具体分析过程为：根据当前的荷载和几何效应，计算各分析单元的平面内和平面外刚度矩阵，分别组成结构的整体平面内和平面外刚度矩阵，施加边界条件，若平面内刚度≤0，则改用较小的荷载增量重复该循环分析；否则检查平面外刚度矩阵，若平面外刚度矩阵≤0，则改用较小的荷载增量重复该分析。若结构平面内平面外稳定均满足，应用该增量荷载求解未知增量位移、增量荷载。最后更新单元的几何和荷载效应，施加下一步增量荷载重复分析直至结构失效。
前文所述平面内分析实质上是对结构在面内荷载作用下的弹性弯曲分析，做出了一些修正以允许轴向力和屈服造成的截面刚度削弱，以及因残余应力、屈服、初弯曲和平面内效应造成的弯曲刚度削弱。但是，对于面内荷载作用下的框架结构的出平面屈曲分析来说，并没有直接的平面外行为，最主要的平面外行为是构件出框架平面外的侧向屈曲。所以，相应的出平面分析应当是一种屈曲分析而不是弯曲分析。如此，则所有的初弯曲和初扭转缺陷应被去除，但其影响可以某种形式考虑。
文献[8]给出了用有限元特征值问题处理平面外屈曲的公式：
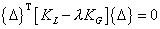（18）
[KL]是平面外刚度矩阵，[KG]是平面外稳定（几何刚度）矩阵，{∆}平面外位移向量。刚度矩阵应当包括由屈服引起的任何削弱效应，稳定矩阵应当允许弯矩分配和荷载关于剪心高度的效应，以及轴向力和弯矩的非弹性重分配。合适的处理节点平面外变形的连续性可以考虑端部约束的效应。
4.2.3 实用的侧向屈曲分析方法—有效刚度法
在目前考虑平面外屈曲的改进塑性铰法高级分析中，以K. Wongkaew和W.F. Chen[15]给出的分别进行平面内和平面外两阶段分析的平面钢框架设计分析方法较为实用。该方法用弹性刚度的有效值代替其弹性值以考虑材料非线性和几何非线性效应对平面外屈曲强度的影响，采用线性稳定函数理论，并用有限元分析方法导出二阶刚度矩阵。设计平面钢框架采用的与非线性相关的假定，在与设计规范构件强度公式保持一致的基础上稍作修正。假定位移和应变足够小，以便线性稳定（二阶）理论可以应用，这是经典稳定理论的基础。非弹性、残余应力和几何缺陷的效应在构件的水平上得以考虑。其具体做法如下面的分节所示。
4.2.3.1 对二阶效应的考虑
要考虑钢框架的平面外位移，一个分析单元需要14个整体自由度才能反映所有可能的位移，每个节点包括三个横向自由度、三个扭转自由度和一个翘曲自由度。图4是荷载效应和相应位移的示意。
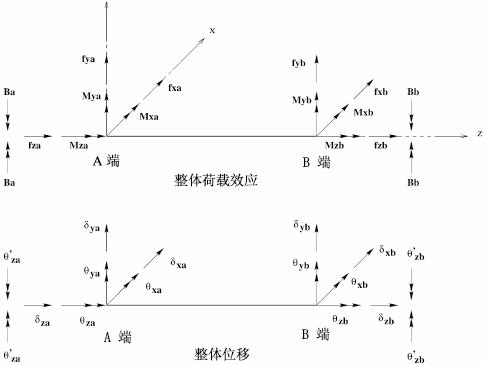
图4 整体荷载效应及整体位移
基于线性稳定假定，Chen、Atsuta和Trahair[49-50]以及其他研究者证明，对于承受平面内荷载的平面框架，在线性状态下其平面内的荷载-位移关系与平面外的分叉屈曲是不耦合的。因此，分析单元的刚度矩阵可以用四个独立的矩阵组成，一个与平面内行为相关，一个与平面外行为相关，另外两个是零矩阵。平衡方程可以用符号表示如下：
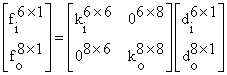（19）
这里的平面内项为：
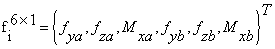（20）
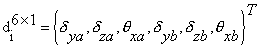（21）
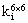是平面内刚度矩阵。平面外项为：
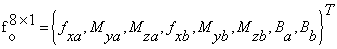（22）
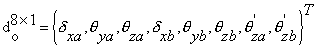（23）
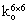是平面外刚度矩阵。平面内刚度矩阵ki的推导主要有两种方法，包括有限元分析法和稳定函数法。但目前正确的平面外刚度矩阵还没有被推导出来，这里用到的平面外二阶刚度矩阵ko是Barsoum和Gallagher[51]用有限元分析方程得出的，推导中用到的假定与经典稳定分析所采用的假定一致。计入平面外荷载效应，用0值替代相应项，平面外二阶刚度矩阵可以表示为：
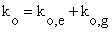（24）
4.2.3.2 对材料非线性和几何缺陷的考虑
用“有效刚度法”考虑所有材料非线性、残余应力和几何缺陷对平面外屈曲的影响，具体做法是将平面外弹性刚度EIy、EIw和GJ用体现剩余弹性核特性的值(EIy)t、(EIw)t、(GJ)t代替。对于几何缺陷造成的额外荷载效应对截面能力的削弱，用进一步减小刚度的方法近似。为了与规范中设计公式一致，用规范中的构件强度公式标定有效刚度的大小，并使有效刚度同时包括几何缺陷和材料非线性两种影响因素的效应。文献[15]给出了具体的梁、柱及压弯构件的等效刚度。
4.2.3.3 对翘曲自由度的处理
由于仅在构件的水平上考虑了翘曲，所以假定单元端部连接处翘曲自由度间要么完全相互制约：在同一连接上的所有单元端部共用一个整体翘曲自由度；要么没有相关作用：每个单元有自己的翘曲自由度，这使每个翘曲自由度产生了一个附加的独立自由度，并允许各单元在连接处有不同的瞧去约束。对于前者可以把每个连接单元与翘曲相关的项直接加入框架刚度矩阵，对后者翘曲约束可以作为边界条件处理。
需要指出的是，严格处理单元端部在连接处的相关作用需要能考虑截面畸变的更先进的分析，需要详细考虑各种连接方式的细节。这种分析的例子见文献[52-53]。
4.3 关于半刚性连接
除了几个特例外，钢框架的连接通常是半刚性的。文献[18,54]讨论了常用连接的特性，文献[18]还总结了几种模拟半刚性连接的弯矩—转角特性的计算公式，详细讨论了半刚性框架的分析。这里仅简单介绍Liew、Kim等在塑性铰高级分析中对半刚性连接的模拟方法。他们把梁柱半刚性连接模拟为零长度转动弹簧，所用的方程允许构件与连接之间产生相对扭转和弯扭。单元端部的连接单元直接作为整体未知量，无需修改单元刚度矩阵，因此便于应用。
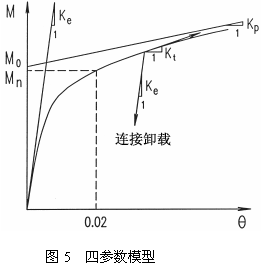
Liew [55]对薄壁管构件钢框架采用了Heish推荐的四参数幂函数模型体现典型连接的弯矩转角关系。其表达式为：
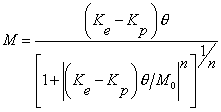（25）
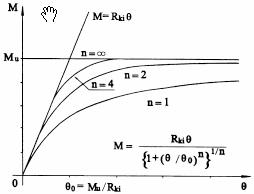
图 6 三参数模型
Ke是连接的初始刚度矩阵，Kp是应变强化刚度矩阵，M0是参考弯矩，n是形状参数。如果有试验数据，公式中的四个参数可以通过曲线拟合得到；如果直到连接的细部情况，也可用分析方程得出。但是一般设计时并不确定连接的具体方式，需要一个基于一般连接试验数据库的标准曲线作为参照，或者使用根据数据库得到的有关参数。Heish的研究报告给出了九种常用连接方式在面内弯曲荷载作用下的四个参数的平均值。
Kim[56]等采用了用三个参数的Kishi-Chen幂函数模型：
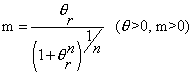（26）
这里的m＝M/Mu，θr＝θ/θ0，θ0＝Mu/Rki，Mu是连接的最大弯矩承载力，Rki是初始连接刚度，n是形状参数。对于公式中的参数，文献给出了四种常见连接的解决方法。
以上两种方法都可以考虑卸载导致的应力重分配对连接的影响。
5 改进塑性铰法的验证对改进塑性铰法精度的验证，一般推荐两种方法，一种是与塑性铰法的分析结果对比，一种是与设计规范的计算结果对比。文献[3,7,14-17,20,22,24]等的对比结果显示改进塑性铰法分析具有较高的精度，能够满足工程设计的要求，可以用于实际设计。
6 结论和建议 塑性区法高级分析尚有待简化，比如使用包括梁柱单元的混合单元，才能普遍用于实际工程设计。改进塑性铰法作为一种可行的整体分析方法，已能够考虑二阶非线性、几何非线性、材料非线性、连接非线性等影响钢框架的强度和稳定的关键因素，有望成为钢框架工程设计的实用方法。
本文首先介绍了有关高级分析的一些基本情况，然后分别针对平面框架的平面内分析和平面外分析，详细介绍了改进塑性铰法对各种非线性问题的处理方法。文中还介绍了对梁、柱、压弯构件和二维钢框架结构非线性分析的现状。对构件的非弹性平面外屈曲，尤其是双向压弯构件的屈曲，研究并不充分，针对二维框架的非弹性研究也不多。此外，很少有人在高级分析中研究弱轴弯曲的问题。
改进塑性铰法用稳定函数法或有限元分析方程推导出单元刚度矩阵，考虑二阶效应的影响。对残余应力、几何缺陷和弯矩的影响等因素也采用近似的方法解决，并保持了较高的精度。用减小切线模量代替减小截面惯性矩近似残余应力造成的截面平面内承载能力削弱，用体现剩余弹性核特性的值(EIy)t、(EIw)t、(GJ)t代替平面外弹性刚度EIy、EIw和GJ，以有效刚度法体现所有材料非线性、残余应力和几何缺陷造成的平面外能力的削弱等等，这种近似解决的方法证明是可行的。
改进塑性铰法为了简化计算和分析，将一个构件用一个或者二三个单元分析。由于没有在截面上划分分区单元，很难考虑局部屈曲和截面翘曲这种需要详细分析截面各纤维受力状态的问题。对于影响结构强度的关键构件或连接，应当用塑性分配法。而要考虑非弹性侧向屈曲，包括局部屈曲和翘曲的塑性效应，必须改变现在使用的三参数塑性强度公式。一个可能的解决方法是在塑性分配法中使用壳单元，这种单元不但便于解决翼缘或腹板的局部屈曲，还能够很好的考虑构件的侧向扭转和翘曲效应。
严格意义上的空间钢框框架二阶弹塑性分析似乎还未出现。要真正在结构水平上分析钢框架在不同荷载水平下的行为和失效模式，需计及弯扭屈曲，解决具有双向弯曲和扭转并相互耦联的更为复杂的三维空间刚架的弹塑性稳定问题，还需要考虑结构的整体扭转、最不利的荷载组合、荷载相对剪心的距离以及各个构件最不利的几何缺陷形式等复杂问题。
参考文献
[1] W.F. Chen and S. Toma, “Advanced Analysis of Steel Frames—Theory, Software, and Application”, CRC Press INC,1996
[2] Chen W.F. and Kim S.E., “LRFD Steel Design Using Advanced Analysis”, CRC Press INC,1997
[3] 陈骥, “刚架平面稳定的整体设计法”,钢结构,2003年第4期,第18卷,总第66期:46-50
[4] SA,AS4100, “Steel Structures”,Standards Australia,Sydney,1998.
[5] Eurocode 3, “Design of Steel Structures”, Part 1, General Rules and Rules for Buildings, Brussels, 1992
[6] W.F. Chen, “Structural stability: from theory to practice”, Engineering Structures, 22(2000):116-122
[7] W.F. Chen, Seung-Eock Kim, Se-Hyu Choi, “Practical Second Order Inelastic Analysis for Three-Dimensional Steel Frames, Steel Structures”,1 (2001):213-223
[8] N.S. Trahair, S.-L. Chan, “Out-of-plane advanced analysis of steel structures”, Engineering Structures 25 (2003):1627–1637
[9] Clarke MJ, Bridge RQ, Hancock GJ, Trahair NJ, “Advanced analysis of steel building frames”, Journal of Constructional steel research 1992; 23(1-3):1-30
[10] 陈骥,《钢结构稳定—理论与设计》，第二版，北京，科学出版社,2003
[11] Deierlein GG，“Steel-framed structures”， Progress in structural engineering and materials”, Vol.1, NO.1, London: CRC Ltd., September 1997
[12] White D W，“Plastic-Hinge Methods for Advanced Analysis of Steel Frames. Journal of Constructional Steel Research,1993,24(2):121～152
[13] White DW, Chen WF, “Plastic-hinge based methods for advanced analysis and design of steel frames”, Bethlehem, PA:Structural Stability Research Council, Lehigh University,1993
[14] Seung-Eock Kim, Jaehong Lee, “Improved refined plastic-hinge analysis accounting for lateral torsional buckling”, Journal of Constructional Steel Research 58 (2002):1431–1453
[15] K. Wongkaew, W.-F. Chen, “Consideration of out-of-plane buckling in advanced analysis for planar steel frame design”, Journal of Constructional Steel Research 58 (2002):943–965
[16] J.Y. Richard Liew, L.K. Tang, “Advanced plastic hinge analysis for the design of tubular space frames”, Engineering Structures 22 (2000):769–783
[17] Seung-Eock Kim, Moon-Ho Park , Se-Hyu Choi, “Direct design of three-dimensional frames using practical advanced analysis”, Engineering Structures 23 (2001): 1491–1502
[18] 陈惠发著，周绥平译，《钢框架稳定设计》，世界图书出版社1999.8
[19] J. Y. Richard Liew, D. W. White and W. F. Chen, “Limit states design of semi-rigid frames using advanced analysis: Part 1: Connection modeling and classification”, Journal of Constructional Steel Research, Volume 26, Issue 1, 1993: 1-27
[20] Seung-Eock Kim and Wai-Fah Chen, “Practical advanced analysis for semi-rigid frame design”, Engineering Journal, Fourth Quarter,1996:129-141
[21] W.F. Chen and Yoshiaki Goto and J.Y. Richard Liew, “Stability Design of Semi-Rigid Frame”,John Wiley & Sons, Inc, 1996
[22] Seung-Eock Kim, Se-Hyu Choi, “Practical advanced analysis for semi-rigid space frames”, International Journal of Solids and Structures,38(2001):9111-9131
[23] N. Kishi, W.F. Chen and Y. Goto, “Effective Length Factor of Columns in Semirigid and Unbraced Frame”,Journal of Structure Engineering Vol. 123，No.3，March,1997:313-321
[24] Seung-Eock Kim, Jaehong Lee, Joo-Soo Park, “3-D second-order plastic-hinge analysis accounting for local buckling”, Engineering Structures, 25 (2003):81-90
[25] Seung-Eock Kim, Moon Kyum Kim, Wai-Fah Chen, “Improved refined plastic hinge analysis accounting for strain reversal”, Engineering Structures 22 (2000):15-25
[26] Seung-Eock Kim and Wai-Fah Chen, “Further studies of practical advanced analysis for weak-axis bending”, Engineering Structures,Vol. 19, No. 6 1997:407-416
[27] Chen I-Hong, and Chen Wai-Fah, “Major design impact of 1997 LRFD steel seismic code revision in USA”, Journal of Structure Engineering Vol.27，No.1，April, 2000:1-16
[28] Vogel U. “Calibrating frames”, Stahlbau 1985,54:295-301.
[29] Philip Avery, Mahen Mahendran, “Distributed plasticity analysis of steel frame structures comprising non-compact sections”, Engineering Structures 22 (2000): 901–919
[30] Avery P, Mahendran M, “Large scale testing of steel frame structures comprising non-compact sections”, Engineering Structures, 2000,22:920–936
[31] Xiao-Mo. Jiang, Hong. Chen, J.Y. Richard. Liew, “Spread-of-plasticity analysis of three-dimensional steel Frames”, Journal of Constructional Steel Research 58(2002):193-212
[32] Yeong-BY, Kuo-SR, “Theory and Analysis of Nonlinear Frame Structure”,Prentice Hall, 1994
[33] Buonopane, S.G., Schafer, B.W., Igusa, T, “Reliability Implications of Advanced Analysis in Design of Steel Frames”, Annual Technical Session and Meeting, Structural Stability Research Council, April, 2003. Baltimore, MD.
[34] 王孟鸿,《三维空间钢结构高级分析理论与应用》,西安建筑科技大学博士学位论文,2003
[35] 舒兴平,沈蒲生,尚守平，“钢框架结构二阶弹塑性稳定极限承载力试验研究”，钢结构，1999年第4期：19-22
[36] 舒兴平,尚守平, “平面钢框架结构二阶弹塑性分析”, 钢结构,第15卷, 2000年第1期：24-27
[37] 郭兵,陈爱国, “半刚接钢框架的有限元分析及性能探讨”,建筑结构学报,第22卷第5期2001年10月:48-52
[38] 顾正维, “钢结构半刚性连接的非线性分析”, 浙江大学博士学位论文,2003
[39] 王新武,《钢框架梁柱连接研究》,武汉理工大学博士学位论文,2003
[40] 沈世钊，陈昕，《网壳结构稳定性》，科学出版社，1999
[41] 董石麟,钱若军,《空间网格结构分析理论与计算方法》,中国建筑工业出版社，2000.08
[42] 张文元,张耀春，“高层钢结构双重非线性分析的塑性铰法”,哈尔滨建筑大学学报，Vol.33:2-7
[43] 张文元,张耀春，“空间受力钢柱的双重非线性分析”,哈尔滨建筑大学学报，Vol-33, No.6,2000:8-12
[44] 李君,张耀春, “高层钢结构的非线性动力全过程分析方法”, 哈尔滨建筑大学学报,第33卷第1期2000年2期:16-19
[45] 尹德钰,刘善维,钱若军,《网壳结构设计》，中国建筑工业出版社，1996
[46] 苏明周，顾强，申林, “钢构件在循环大应变作用下的有限元分析”,工程力学，Vol.18 No.4:51-59
[47] 徐伟良,潘立本, “钢框架弹塑性大位移分析的单元刚度矩阵”，重庆建筑大学学报，第20卷第4期:28-34。
[48] 许红胜，周绪红，舒兴平, “空间钢框架几何非线性分析的一种新单元”,工程力学第 20卷第4期2003年8月:39-44
[49] Chen W-F, Atsuta T, “Theory of beam-columns”, vol. 2. New York(NY),McGraw-Hill, 1997
[50] Trahair NS, “Flexural–torsional buckling of structures”, Boca Raton (FL), CRC Press, 1993
[51] Barsoum RS, Gallagher RH. Finite element analysis of torsional and lateral stability problems. International Journal for Numerical Methods in Engineering 1970,2:335-52.
[52] Vacharajittiphan P, Trahair NS, “Warping and distortion at i-section joints”, Journal of the Structural Division 1974,100(ST3):547–64.
[53] Krenk S, Damkilde L, “Warping of joints in i-beam assemblages”, Journal of Engineering Mechanics 1991,117(11):2457–74.
[54] 陈绍蕃,《钢结构设计原理》,科学出版社,1997
[55] J.Y. Richard Liew, W.F. Chen, H. Chen，“Advanced inelastic analysis of frame structures”， Journal of Constructional Steel Research 55(2000):245-265
[56] Seung-Eock Kim, Se-Hyu Choi, “Practical advanced analysis for semi-rigid space frames”, International Journal of Solids and Structures 38(2001):9111-9131
原文网址：http://www.pipcn.com/research/200603/8489.htm
也许您还喜欢阅读：