请告诉我们您的知识需求以及对本站的评价与建议。
满意 不满意
Email:
钢筋混凝土模型框架振动台试验分析和抗震性能评估
栏目最新
- 建筑结构鉴定与加固改造技术的进展
- 公路工程养护管理体制问题的思考
- 某小高层纠倾加固技术
- 运用“破窗理论”,搞好高校物业管理
- 5.12地震后震区农村建筑物震害分析和对策
- 对影响建筑寿命因素的探讨
- 建筑修复也是一种挑战
- 淮安市楚州医院病房楼走廊吊顶发霉与结露分析
- 火灾报警控制系统设计在建筑中的应用
- 某工程地下室墙板裂缝原因分析与处理措施
网站最新
内容提示:以同济大学国家防灾减灾重点实验室进行的1/10模型比例的12层钢筋混凝土模型框架振动台模型试验为背景,采用钢筋混凝土结构基于性能的抗震设计理论,分别利用能力谱法和改进的能力谱法对模型框架进行抗震评估,结果表明能力谱法在迭代计算过程中可能不收敛,而改进的能力谱法则可以求出结构在弹性以及弹塑性阶段的性能点。结合对该结构进行的模型振动台试验,并对该结构进行非线性时程分析,结果表明,对于高层建筑改进的能力谱会高估结构的抗震能力。
1 引言
随着基于性能抗震设计理论逐步被地震工程界所认同,对其研究已成为当前地震工程界的热点。在对结构进行基于性能的抗震评估时,目前常用的方法有等效位移法、直接基于位移的方法、能力谱法、非线性静力分析方法、模态推覆分析方法、增量动力分析方法等[1~7]。(参考《建筑中文网》)
本文简要介绍了同济大学 12 层钢筋混凝土框架模型振动台实验,分析了模型结构在不同地震水准时的动力反应,然后利用能力谱法和时程分析法对其进行了抗震评估。
2 振动台模型实验简介[8]
2. 1 模型设计
结构模型是以要研究的工程为原型,运用相似理论确定各有关物理量的缩小比例,并按此比例进行模型的设计和制作;然后对模型结构施加荷载并测量其反应,据此来推断原型结构的反应,如图 1 所示。

图 1 振动台模型试验
2. 2 试验地震波形的选取
试验选用地震波有:El_Centro 波、Kobe 波、上海人工波及上海基岩波。地震的输入方式分 3 种情况,即单向水平输入、正交双向水平输入和正交双向水平和竖向同时输入。本文主要选用 El_Centro 波、Kobe 波、上海人工波和上海基岩波,沿 X 方向单向输入进行研究。
2.3 实验测点布置以及实验现象
试验中采用加速度计、应变传感器量测模型结构的动力响应。加速度计的方向有 X、Y、Z3 个方向。试验中,在 X 向加速度峰值为 0.090g,Y 向加速度峰值为 0.077g,在模型结构上没有发现任何裂缝。在上海人工波(X 单向)加速度峰值为 0.258g 后,在 4层平行于 X 振动方向的框架梁的梁端首先出现细微的自上而下和自下而上发展的垂直裂缝,缝宽小于0.05mm。在第 El_Centro 波(X 单向)加速度峰值为0.388g 后,平行于 X 振动方向的 4 层~6 层框架梁的梁端均有垂直裂缝,缝宽约 0.08mm,各柱中未观察到裂缝;平行于 Y 振动方向的框架梁柱中也未发现裂缝。在上海人工波(X 单向)加速度峰值为 0.388g后,平行于 X 振动方向的 3 层~6 层框架梁的梁端垂直裂缝贯通,最大缝宽在第 4 层处,约 0.15mm。在El_Centro 波(X,Y 双向)X 向加速度峰值为 0.388g,Y向加速度峰值为 0.329g 后,平行于 Y 振动方向的框架中,于第 4 层~6 层梁的梁端先出现垂直裂缝,缝宽约 0.08mm。之后,随着输入激励加大,梁端裂缝增大,开裂的梁的位置向上层、向下层发展。试验结束时,模型已成为不稳定的机动结构。
2.4 模型结构的动力反应分析
2.4.1模型结构加速度反应
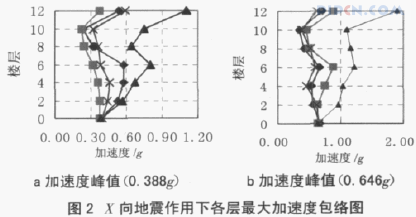
根据各楼层加速度反应时程,可得到模型结构的加速度反应最大值部分列于表 1,部分最大加速度包络图如图 2 所示。分析可知:①模型结构各楼层最大加速度包络图沿高度具有一致的变化规律。②在各次试验工况过程中,结构的上部动力反应较中下部强烈,顶层加速度反应最大,说明高振型影响是比较明显的。③输入地震波的不同,模型各层加速度也不同,四条地震波引起的结构加速度反应程度不等。总体而言,上海人工波引起的结构动力反应最大,同时说明地震波的选择对结构动力反应的影响比较明显。
2.4.2模型结构位移反应
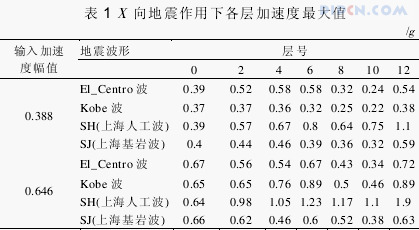
将各层测得的位移时程与台面测得的位移时程相减,即为各层相对于振动台台面的相对位移时程。图3 分别给出 0.258g,0.517g,0.775g 的最大相对位移包络图和层间位移角包络图。由图可知,层间位移曲线呈弯剪型,最大层间位移角发生在结构的 2层~4 层,与多层框架不同,最大层间位移发生在底层,说明随框架高度的增大,结构高宽比和高振型的影响显著,使结构的破坏位置发生变化。
3 框架结构抗震性能对比分析
3.1 Pushover 分析
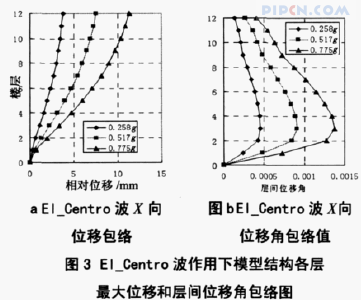
本文以模型框架结构为原型,采用非线性有限元计算分析软件 SAP2000,建立三维有限元模型进行静力弹塑性分析。框架结构在均匀分布、倒三角分布和指数分布的侧向力作用下,平面框架的塑性铰出现位置相差不大,图 4 为水平侧向力模式为指数分布时塑性铰出现位置及发展图。由图可知,随着水平荷载的增大,结构经历了混凝土开裂、出现一个塑性铰,出现多个塑性铰,直至最后出现足够多的塑性铰,使结构成为几何可变的机构而发生破坏。由图可知,大多数塑性铰发生在梁端,但模型结构的最终破坏模式为以梁铰为主的混合侧移机构,结构的薄弱部位在 2 层 ~8 层,与试验现象是相吻合的。每一状态所对应的基底剪力 - 顶点位移见表 2。
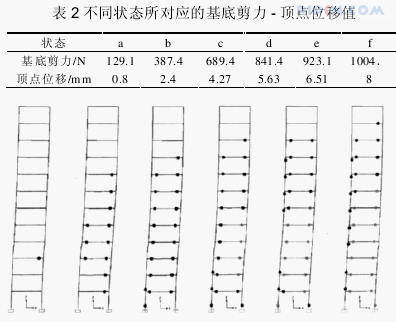
图4 结构破坏模式发展图
3.2 用能力谱法进行抗震性能评估
本文仅对 El_Centro 波作用的工况,其加速度峰值分别为 0.1g、0.2g、0.3g 和 0.35g 等 4 种情况进行分析。分别用与阻尼有关的能力谱法和改进的能力谱法对结构进行抗震评估。
(1)用与阻尼有关的能力谱法进行抗震性能评估
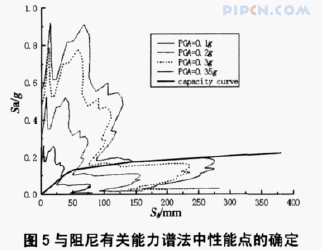
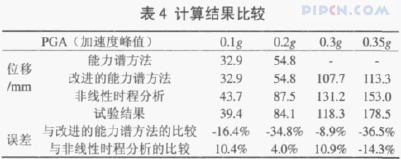
不同加速度峰值时,该结构在阻尼比为 5%时的能力谱如图 5 所示。由图可知,当加速度峰值为0.1g、0.2g 时,结构处在弹性阶段,没有发生屈服,性能 点 的 坐 标 分 别 为(Sd,Sa)=(32.9 mm,0.091g),(54.8mm,0.134g);而当加速度峰值为 0.3g、0.35g 时,结构进入屈服阶段,阻尼比及基本周期发生变化,需要计算等效周期与等效阻尼比,确定结构的性能点。其计算过程是一个迭代过程,见表 3。由表 3 可知,加速度峰值为 0.3g、0.35g 时,计算结果是不收敛的。可见,用与阻尼有关的能力谱法对该结构进行抗震评估,在弹性范围是可行的,而在非弹性范围其计算结果可能不收敛,这时,应采用改进的能力谱法评估该结构。
2)用与位移延性有关的能力谱法进行抗震性能评估
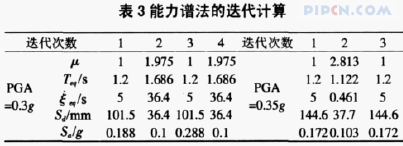
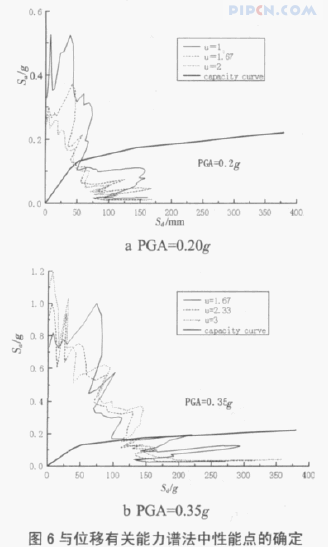
该结构的屈服位移为 uy=54.4mm,分别作出不同位移延性时 El_Centro 波的需求曲线,如图 6 所示。先求出需求曲线与该结构能力曲线的交点值,然后由交点的位移值 Sd 与结构的屈服位移相比,若得到的延性系数与该位移延性需求曲线的延性系数相符和,则该交点即为结构的性能点。例如,在加速度峰值为 0.35g 时,结构的性能点位移值为 113.3mm,对应的加速度值为 0.159g。同理,可以求出在加速度峰值为 0.2g、0.3g 时结构的性能点,对应的性能点坐标分别为:(54.8mm,0.134g) 和(107.7mm,0.153g)。其中峰值加速度为 0.2g 时的性能点与用与阻尼比相关的能力谱法求得的结果一致。综上所述,该结构在不同峰值加速度下得到的顶层位移值,以及由试验得到的加速度时程曲线经积分转换后得到的位移最大值,如表 4 所示。另采用试验中的 El_Centro 波,把峰值加速度分别调整到0.1g、0.2g、0.3g 和 0.35g,对该结构进行非线性时程分析,得到的顶层位移最大值也见表 4 所示。
4 结论
1)在弹性阶段和接近屈服阶段时程分析得到的顶层位移和层间位移角与试验结果吻合较好,在结构屈服后,两者出现一定偏差,这是由时程分析采用的滞回模型与实际结构破坏情况的偏差造成的。
2) 由于静力弹塑性 push-over 分析方法没有考虑地震荷载反复作用下结构的非弹性变形的累积效应,有可能低估杆端的塑性转角。随框架高度的增大,结构高宽比和高振型的影响显著,静力弹塑性push-over 分析方法用于高层结构的抗震性能评估会造成一定的误差。
3)能力谱法和改进的能力谱法对高层结构进行性能评估时误差较大,改进的能力谱法会高估结构的抗震能力,特别是在加速度峰值较大时,其误差可达到 30%。对高层建筑进行抗震评估,改进的能力谱法是可行,但需要对评估误差进行适当处理,以使评估结果更准确。
【参考文献】
【1】MervynJKowalsky,MJNigelPriestley,GregoryAMacrae.Displacement 2based design of RC bridge columns in seismicregions[J].EarthquakeEngineeringandStructuralDynamics,1995,24(12):1623-1643.
【2】MSMedhekar,DJLKennedy.Displacement2basedseismicdesignofbuildings2theory[J].EngineeringStructures,2000,22(3):201-209.
【3】TB Panagiotakos,M N Fardis. A displacement based seismicdesign procedure for RC building and comparison with EC8 [J] .Earthquake Engineering and Structural Dynamics , 2001 , 30 (10) :1439-1462.
随着基于性能抗震设计理论逐步被地震工程界所认同,对其研究已成为当前地震工程界的热点。在对结构进行基于性能的抗震评估时,目前常用的方法有等效位移法、直接基于位移的方法、能力谱法、非线性静力分析方法、模态推覆分析方法、增量动力分析方法等[1~7]。(参考《建筑中文网》)
本文简要介绍了同济大学 12 层钢筋混凝土框架模型振动台实验,分析了模型结构在不同地震水准时的动力反应,然后利用能力谱法和时程分析法对其进行了抗震评估。
2 振动台模型实验简介[8]
2. 1 模型设计
结构模型是以要研究的工程为原型,运用相似理论确定各有关物理量的缩小比例,并按此比例进行模型的设计和制作;然后对模型结构施加荷载并测量其反应,据此来推断原型结构的反应,如图 1 所示。

图 1 振动台模型试验
2. 2 试验地震波形的选取
试验选用地震波有:El_Centro 波、Kobe 波、上海人工波及上海基岩波。地震的输入方式分 3 种情况,即单向水平输入、正交双向水平输入和正交双向水平和竖向同时输入。本文主要选用 El_Centro 波、Kobe 波、上海人工波和上海基岩波,沿 X 方向单向输入进行研究。
2.3 实验测点布置以及实验现象
试验中采用加速度计、应变传感器量测模型结构的动力响应。加速度计的方向有 X、Y、Z3 个方向。试验中,在 X 向加速度峰值为 0.090g,Y 向加速度峰值为 0.077g,在模型结构上没有发现任何裂缝。在上海人工波(X 单向)加速度峰值为 0.258g 后,在 4层平行于 X 振动方向的框架梁的梁端首先出现细微的自上而下和自下而上发展的垂直裂缝,缝宽小于0.05mm。在第 El_Centro 波(X 单向)加速度峰值为0.388g 后,平行于 X 振动方向的 4 层~6 层框架梁的梁端均有垂直裂缝,缝宽约 0.08mm,各柱中未观察到裂缝;平行于 Y 振动方向的框架梁柱中也未发现裂缝。在上海人工波(X 单向)加速度峰值为 0.388g后,平行于 X 振动方向的 3 层~6 层框架梁的梁端垂直裂缝贯通,最大缝宽在第 4 层处,约 0.15mm。在El_Centro 波(X,Y 双向)X 向加速度峰值为 0.388g,Y向加速度峰值为 0.329g 后,平行于 Y 振动方向的框架中,于第 4 层~6 层梁的梁端先出现垂直裂缝,缝宽约 0.08mm。之后,随着输入激励加大,梁端裂缝增大,开裂的梁的位置向上层、向下层发展。试验结束时,模型已成为不稳定的机动结构。
2.4 模型结构的动力反应分析
2.4.1模型结构加速度反应

根据各楼层加速度反应时程,可得到模型结构的加速度反应最大值部分列于表 1,部分最大加速度包络图如图 2 所示。分析可知:①模型结构各楼层最大加速度包络图沿高度具有一致的变化规律。②在各次试验工况过程中,结构的上部动力反应较中下部强烈,顶层加速度反应最大,说明高振型影响是比较明显的。③输入地震波的不同,模型各层加速度也不同,四条地震波引起的结构加速度反应程度不等。总体而言,上海人工波引起的结构动力反应最大,同时说明地震波的选择对结构动力反应的影响比较明显。

2.4.2模型结构位移反应
将各层测得的位移时程与台面测得的位移时程相减,即为各层相对于振动台台面的相对位移时程。图3 分别给出 0.258g,0.517g,0.775g 的最大相对位移包络图和层间位移角包络图。由图可知,层间位移曲线呈弯剪型,最大层间位移角发生在结构的 2层~4 层,与多层框架不同,最大层间位移发生在底层,说明随框架高度的增大,结构高宽比和高振型的影响显著,使结构的破坏位置发生变化。

3 框架结构抗震性能对比分析
3.1 Pushover 分析
本文以模型框架结构为原型,采用非线性有限元计算分析软件 SAP2000,建立三维有限元模型进行静力弹塑性分析。框架结构在均匀分布、倒三角分布和指数分布的侧向力作用下,平面框架的塑性铰出现位置相差不大,图 4 为水平侧向力模式为指数分布时塑性铰出现位置及发展图。由图可知,随着水平荷载的增大,结构经历了混凝土开裂、出现一个塑性铰,出现多个塑性铰,直至最后出现足够多的塑性铰,使结构成为几何可变的机构而发生破坏。由图可知,大多数塑性铰发生在梁端,但模型结构的最终破坏模式为以梁铰为主的混合侧移机构,结构的薄弱部位在 2 层 ~8 层,与试验现象是相吻合的。每一状态所对应的基底剪力 - 顶点位移见表 2。

图4 结构破坏模式发展图
3.2 用能力谱法进行抗震性能评估
本文仅对 El_Centro 波作用的工况,其加速度峰值分别为 0.1g、0.2g、0.3g 和 0.35g 等 4 种情况进行分析。分别用与阻尼有关的能力谱法和改进的能力谱法对结构进行抗震评估。
(1)用与阻尼有关的能力谱法进行抗震性能评估

不同加速度峰值时,该结构在阻尼比为 5%时的能力谱如图 5 所示。由图可知,当加速度峰值为0.1g、0.2g 时,结构处在弹性阶段,没有发生屈服,性能 点 的 坐 标 分 别 为(Sd,Sa)=(32.9 mm,0.091g),(54.8mm,0.134g);而当加速度峰值为 0.3g、0.35g 时,结构进入屈服阶段,阻尼比及基本周期发生变化,需要计算等效周期与等效阻尼比,确定结构的性能点。其计算过程是一个迭代过程,见表 3。由表 3 可知,加速度峰值为 0.3g、0.35g 时,计算结果是不收敛的。可见,用与阻尼有关的能力谱法对该结构进行抗震评估,在弹性范围是可行的,而在非弹性范围其计算结果可能不收敛,这时,应采用改进的能力谱法评估该结构。

2)用与位移延性有关的能力谱法进行抗震性能评估
该结构的屈服位移为 uy=54.4mm,分别作出不同位移延性时 El_Centro 波的需求曲线,如图 6 所示。先求出需求曲线与该结构能力曲线的交点值,然后由交点的位移值 Sd 与结构的屈服位移相比,若得到的延性系数与该位移延性需求曲线的延性系数相符和,则该交点即为结构的性能点。例如,在加速度峰值为 0.35g 时,结构的性能点位移值为 113.3mm,对应的加速度值为 0.159g。同理,可以求出在加速度峰值为 0.2g、0.3g 时结构的性能点,对应的性能点坐标分别为:(54.8mm,0.134g) 和(107.7mm,0.153g)。其中峰值加速度为 0.2g 时的性能点与用与阻尼比相关的能力谱法求得的结果一致。综上所述,该结构在不同峰值加速度下得到的顶层位移值,以及由试验得到的加速度时程曲线经积分转换后得到的位移最大值,如表 4 所示。另采用试验中的 El_Centro 波,把峰值加速度分别调整到0.1g、0.2g、0.3g 和 0.35g,对该结构进行非线性时程分析,得到的顶层位移最大值也见表 4 所示。


4 结论
1)在弹性阶段和接近屈服阶段时程分析得到的顶层位移和层间位移角与试验结果吻合较好,在结构屈服后,两者出现一定偏差,这是由时程分析采用的滞回模型与实际结构破坏情况的偏差造成的。
2) 由于静力弹塑性 push-over 分析方法没有考虑地震荷载反复作用下结构的非弹性变形的累积效应,有可能低估杆端的塑性转角。随框架高度的增大,结构高宽比和高振型的影响显著,静力弹塑性push-over 分析方法用于高层结构的抗震性能评估会造成一定的误差。
3)能力谱法和改进的能力谱法对高层结构进行性能评估时误差较大,改进的能力谱法会高估结构的抗震能力,特别是在加速度峰值较大时,其误差可达到 30%。对高层建筑进行抗震评估,改进的能力谱法是可行,但需要对评估误差进行适当处理,以使评估结果更准确。
【参考文献】
【1】MervynJKowalsky,MJNigelPriestley,GregoryAMacrae.Displacement 2based design of RC bridge columns in seismicregions[J].EarthquakeEngineeringandStructuralDynamics,1995,24(12):1623-1643.
【2】MSMedhekar,DJLKennedy.Displacement2basedseismicdesignofbuildings2theory[J].EngineeringStructures,2000,22(3):201-209.
【3】TB Panagiotakos,M N Fardis. A displacement based seismicdesign procedure for RC building and comparison with EC8 [J] .Earthquake Engineering and Structural Dynamics , 2001 , 30 (10) :1439-1462.
原文网址:http://www.pipcn.com/research/201101/14735.htm
也许您还喜欢阅读:
