请告诉我们您的知识需求以及对本站的评价与建议。
满意 不满意
Email:
关于墙体传热量的两种计算方法的比较
栏目最新
- 低碳节能建筑设计的相关问题及解决方法
- 江苏建筑职业技术学院图书馆设计文化理念
- 四川雅安名山县涌泉村抗震小学的设计理念
- 四川汶川5.12大地震的启示
- 汶川大地震震中纪念馆的创作思考
- 洛阳洛南新区雅安新城结构设计
- 绿色居住建筑的节地设计
- 广州珠江新城海心沙地下空间建筑设计方案
- 黔东南地区郎德苗寨民居的热适应性
- 西气东输工程中长输管道站场建筑模块化设计与应用
网站最新
内容提示：有关墙体传热量计算的方法是随着人们对房间负荷计算精度要求的不断提高而不断发展的，大概经历了谐波法、反应系数法和Z传递系数法（或者冷负荷系数法）。本文通过举例比较了前两种方法应用于墙体传热计算的异同，并作出了直观曲线图加以比较。
摘要：有关墙体传热量计算的方法是随着人们对房间负荷计算精度要求的不断提高而不断发展的，大概经历了谐波法、反应系数法和Z传递系数法（或者冷负荷系数法）。本文通过举例比较了前两种方法应用于墙体传热计算的异同，并作出了直观曲线图加以比较。（参考《建筑中文网》）
关键词：冷负荷 谐波法 反应系数法
人们对房间内环境舒适性要求的不断提高，反映在冷负荷计算方面就是计算方法的不断进步，先后出现了谐波法、反应系数法、Z传递函数法，冷负荷系数法则是建立在Z传递函数法基础上的一种适合手算的计算方法。而计算机技术的飞速发展使得负荷计算朝着精确化、动态化、可控化方向不断发展。
由内外维护结构隔离出来的空间——房间构成了建筑物的基本单元。我们根据控制论中的线性系统理论来研究房间的热过程时，把房间的围护结构以外墙为代表构成一个墙体热力系统，墙的外侧空气温度和太阳辐射是该系统的扰量，墙的传热量是该系统的反应；再把房间的各个内表面和室内空气看成一个热力系统，可以近似当作一个线性系统，称作房间热力系统。
下面本文从两种方法入手，通过对一具体墙体传热实例进行的计算，对其结果进行分析比较。
1 谐波反应法1.1 背景介绍
谐波法出现在准稳态传热计算时期的后期,并建立在早期的当量温差计算方法的基础之上。最早追溯到50年代初，苏联的A .T .Щ κοποвер 等人提出了谐波分解的类似方程，并用衰减度和延迟时间来表示。
谐波法可以建立在墙体导热方程经典求解的基础之上，早在40年代已经提出。本文用系统的频率响应来讨论周期性传热，因为谐波法有周期扰量的前提，所以该方法基本只适用于冷负荷的设计计算。
1.2.1 墙体热力系统的频率响应
首先对外部温度扰量的谐波分解的指数表达式为：
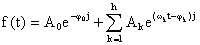(1.1)
以谐波为扰量的系统数学模型为：
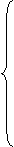
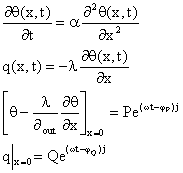
（1.2）
说明：
1. 式1.2中的一对温度和热流扰量只是振幅和初始相位不同的同阶谐量。
2. 当数模的边界条件改为墙体两侧的温度，内侧维持稳定时，仍可推得上述结论，而且采用过余温度的结果，可以取内侧温度为零，因此在求取传热量时只要考虑系统的传热传递函数及传热过程的频率响应。
3. 对多层墙体同样可以把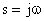
代入相应传递函数来求其频率响应。
1.2.2 墙体传热量计算公式
当扰量为式（1.1）的多阶谐波时,根据过余温度定义,其首项零阶谐波外侧平均温度与室内气温之差：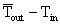
。第k阶谐波的传递函数记为
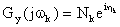（1.3）
则第k阶谐波的传热量:
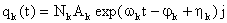（1.4）
对于零阶谐波，因为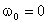
， 
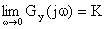， K为墙体传热系数，从而零阶谐波的传热量为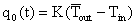 
墙体总传热量为：
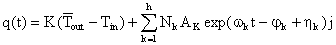（1.5）
1.3 衰减度和延迟时间
衰减度和延迟时间是使得谐波法的物理意义更加直观的两个重要参数,下面的内容是基于有限厚墙体来讨论的。
定义墙体外侧综合温度（设为周期扰量）的波幅与内表面温度波幅的比值为该墙体的衰减度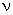
，内表面温度波对外侧综合温度波的相位滞后为该墙体的延迟时间
。
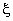对于单墙体，已求得内表面热流公式（1.4）,采用过余温度,设室温为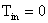
，则根据牛顿放热定律，内表面温度为：
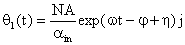
故墙体的衰减度和延迟时间为：
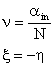（1.14）
式中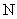
和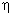
为传热传递函数
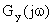的模和幅角，对于带有两侧空气边界层的单层匀质墙，则可用式（1.9）和(1.10)进行运算. 第k阶谐波的墙体衰减度
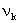和延迟时间可取
=
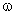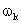来计算。
这样，墙体传热式可用它的衰减度和延迟时间来改写，其实部为：
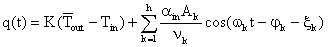（1.15）
1.4 例题
已知某平屋顶是厚为150mm的钢筋混凝土板,其密度为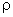
=2500kg/m3 ，导热系数：
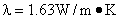，比热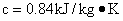
。内外表面放热系数给定为
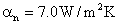和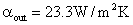
。试计算该平屋顶的衰减度和延迟时间。并求扰量
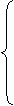
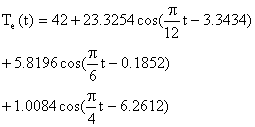的温度作用下,室温维持280C时的单位面积传热量。
依次取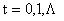
可算得逐时传热量如表1所示。
表1 三阶谐波法计算出的墙体传热值
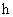 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 一阶传热量 (W/m2) | 40.38 | 26.65 | 14.54 | 4.88 | -1.68 | -4.09 | -3.95 | 0.5 |
| 二阶传热量(W/m2) | 38.322 | 28.1861 | 19.25 | 11.5078 | 5.0889 | 1.0062 | -1.892 | -1.0316 |
| 三阶传热量(W/m2) | 37.7786 | 27.9474 | 19.4622 | 12.0421 | 5.6323 | 1.2404 | -2.1042 | -1.5659 |
| | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 一阶传热量 (W/m2) | 8.34 | 19.06 | 31.90 | 46.01 | 60.42 | 74.15 | 86.26 | 95.92 |
| 二阶传热量(W/m2) | 3.63 | 12.4322 | 25.1311 | 40.9138 | 58.362 | 75.6816 | 90.97 | 102.5478 |
| 三阶传热量(W/m2) | 3.0866 | 12.189 | 25.3433 | 41.4481 | 58.9054 | 75.9185 | 90.7578 | 102.0135 |
| | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 一阶传热量 (W/m2 | 102.48 | 105.49 | 104.75 | 100.3 | 92.46 | 81.74 | 68.90 | 54.78 |
| 二阶传热量(W/m2) | 109.2489 | 110.5862 | 106.808 | 98.7684 | 87.75 | 75.1122 | 62.1311 | 49.6838 |
| 三阶传热量 (W/m2) | 108.7055 | 110.352 | 107.0202 | 99.3027 | 88.2934 | 75.3464 | 61.9189 | 49.1495 |
画出相应的曲线图如图一所示
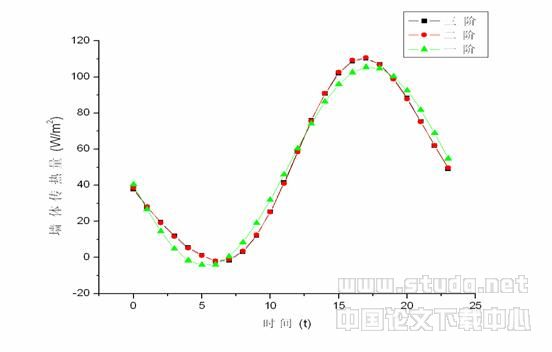
图1 谐波法计算结果曲线示意图
从三者的曲线图我们不难发现:
(1)如果在实际计算中只取一阶谐波进行计算,会导致传热量的波峰和波谷值的偏低。
(2)第二阶和第三阶传热曲线图已经能够很好的吻合，说明在工程计算中，如果不是有特别需要，取阶数为三阶已经足够准确，再高则无意义。
2 反应系数法2.1 背景介绍
反应系数法是加拿大人D.G.Stepphonsen和G.P.Mitalas在60年代末提出来的，该方法将墙体和房间当作线性的热力系统，利用系统传递函数得出某种单位扰量下的各种反应系数,再用反应系数来求解传热量和负荷。
由于反应系数法并不以周期性扰量为前提，可以适用于任意扰量，这是跟谐波法的主要区别，因此反映系数法适用于全年的房间负荷计算模拟。
2.2.1 任意扰量下的墙体传热
作为扰量的室外温度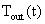
通常以逐时的离散值的形式给出，采用单位三角波或单位矩阵波函数来分离扰量，这两种基本函数，都能归结到单位阶跃函数，这样由于系统的线性定常特点，根据叠加原理和反应对扰量时间延迟的不变性，可把扰量函数
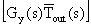的L变换的求解，简化到对单位阶跃扰量下墙体热力系统反应的L变换的求解。
对1.4中的例题，用反应系数法求取单位面积逐时传热量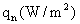
,结果如下表所示。
反应系数法计算出的墙体传热值
 |  |  |  | | | | |
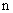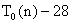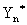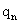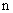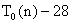| 0 | -3.1 | 0.0398 | 32.1 | 12 | 42.5 | 0.0599 | 63.9 |
| 1 | -3.9 | 0.4190 | 22.9 | 13 | 42.8 | 0.0467 | 81.8 |
| 2 | -4.3 | 0.6236 | 15.1 | 14 | 39.9 | 0.0364 | 97.2 |
| 3 | -4.4 | 0.5455 | 8.6 | 15 | 34.6 | 0.0284 | 108.2 |
| 4 | -3.4 | 0.4352 | 3.3 | 16 | 27.6 | 0.0222 | 113.7 |
| 5 | -0.8 | 0.3410 | -0.4 | 17 | 20.0 | 0.0173 | 113.2 |
| 6 | 3.6 | 0.2662 | -1.8 | 18 | 13.0 | 0.0135 | 107.2 |
| 7 | 9.9 | 0.2076 | -0.1 | 19 | 7.1 | 0.0105 | 96.9 |
| 8 | 17.6 | 0.1619 | 5.4 | 20 | 2.8 | 0.0082 | 83.8 |
| 9 | 25.7 | 0.1263 | 15.1 | 21 | 0.1 | 0.0064 | 69.6 |
| 10 | 33.3 | 0.0985 | 28.8 | 22 | -1.5 | 0.0050 | 55.7 |
| 11 | 39.2 | 0.0768 | 45.6 | 23 | -2.4 | 0.0039 | 43.0 |
相对应传热量曲线图如图2.2所示:
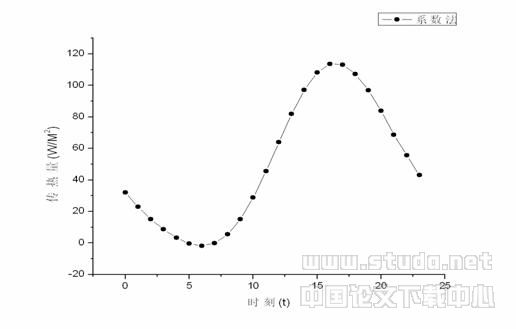
图2 反应系数法传热计算结果曲线图
我们可以将上面例题中两种方法算得的结果作在同一张图中,为了方便读图，图中隐去二阶谐波法计算结果曲线。如图3所示:
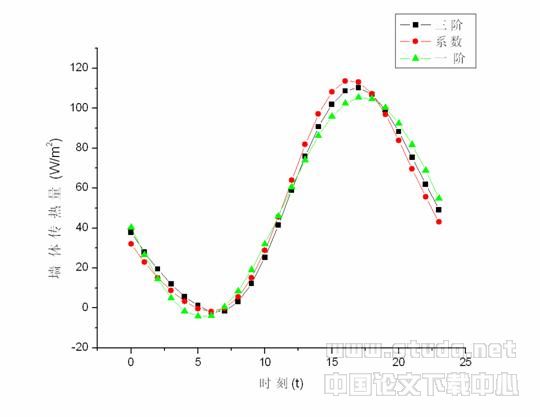
图3 两种方法计算结果的比较
从曲线中可得到：
⑴利用谐波反应法和反应系数法计算出的数值结果非常相近。而谐波法计算出的传热量的最高峰值略低于反应系数法。
⑵从整张曲线图中我们可以直观看出谐波法的曲线较反应系数法滞后,并且三阶谐波相对一阶谐波更加接近反应系数曲线，说明这是公式计算时只采用了三阶以内谐波的缘故。
⑶从原理上我们可以发现，谐波法使用光滑的曲线来近似扰量，而后者则以折线来近似，所以说两者的结果严格来说并不会相等。这一点也可以从上面的曲线图中直观的表现出来。
4 结语本文分别简单介绍了谐波法和反应系数法的背景并作简单推导,利用推导公式计算一实际墙体的传热量,并对结果作出的曲线图作了直观上的比较，总的看来谐波法、反应系数法（及传递函数法）依次是不断进步、不断精确的负荷计算方法。限于篇幅,未对z传递函数法和冷负荷系数法加以比较。
参考文献 [1] 陈友明.多层平板墙体z-传递函数的简单计算方法[J].全国暖通空调制冷2002年学术年会论文集，2002：1119～1122
[2] 曹叔维.房间热过程和空调负荷.上海：上海科学技术文献出版社
[3] 丁鹤龄等.工程数学复变函数.北京：高等教育出版社，1990.9
[4] 张乐法.动态空调负荷计算及其CAD程序发展全史.台北：台湾图文复印社，2001.12
原文网址：http://www.pipcn.com/research/200607/8623.htm
也许您还喜欢阅读：