请告诉我们您的知识需求以及对本站的评价与建议。
满意 不满意
Email:
三跨连续贝雷梁试验
栏目最新
- 东莞至惠州城际铁路隧道安全风险评估与管理
- 高层建筑给排水系统安装施工技术
- 高层建筑施工质量的五个控制要点
- 房屋建筑工程质量问题、原因和防止措施
- 地下停车场防水工程施工质量预控措施
- 试析绿色施工技术在建筑工程中的应用
- 施工企业预算管理措施及案例分析
- 岩溶地区隧道施工综合预报技术案例分析
- 预制块镶面现浇混凝土隧道洞门施工方法
- 建筑施工模板应用技术简析
网站最新
内容提示:本文主要是通过计算国产321桁架的弹性变形、非弹性变形,并测定其挠度,为跨河大桥三跨连续箱梁现浇支架搭设提供技术参数。验证贝雷梁在同一荷载下的理论计算挠度与实际挠度的相符性。
0.引言
跨河大桥跨采用整体现浇施工,由于桥跨跨越河流,施工时为尽量降低对河道通航的防碍,支架在中跨中间设净空 18 米×5 米的通航孔, 在通航孔两侧各设入土 12 米的 21 根 φ0.5 米的钢管桩作临时支点。 拟采用国产 321 公路钢桥桁架(国内通常称为贝雷架)架设连续梁支架,分别支承在桥跨的八个支点处。 为确定支架的实际挠度与理论计算挠度的相符性,需进行三跨连续贝雷梁进行试验。(参考《建筑中文网》)
1.贝雷梁试验
1.1 贝雷梁的假设
计划在桥头路面上布置同高的四个支点,跨度组合为 14+26+14,上搭设单层上下加强 4 排贝雷片,横向每隔 3 米上下采用钢管加固,在贝雷梁上分批采用贝雷片加载。 采用水准仪测其实际的挠度,并与理论计算值相比较。 为比较支点宽度对贝雷梁变形的影响,试验分两次进行,第一次支点宽度约 50CM,即接近点接触状态,第二次支点宽度为4 米,即完全模仿现浇箱梁支架。
1.2 贝雷梁挠度理论值计算
1.2.1 计算中跨 26 米、边跨 14 米连续梁的跨中挠度,计算模型如下
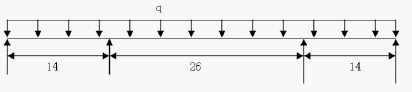
1.2.1.1 让算弯矩分配系数
(1)计算刚度系数(设 EI=26)
iba=EI/L=26/14=1.857 ibc=EI/L=26/14=1.857.
icb=EI/L=26/14=1.857 icd=EI/L=26/14=1.857.
(2)计算弯矩分配系数
在计算某一节点处的分配系数时,相邻的刚结点,应作为临时固端看待。
μba=3iba/(3iba+4ibc)=3×1.857/(3×1.857+4×1)=0.58.
μbc=4ibc/(3iba+4ibc)=4×1.857/(3×1.857+4×1)=0.42.
μcb=4icb/(3icd+4i)=4×1.857 /(3×1.857+4×1)=0.42.
μcd=3icd/(3icd+4icb)=3×1.857/(3×1.857+4×1)=0.58.
1.2.1.2 固端弯矩计算
在连续梁的 B、C 两支点加约束使其固定, 这时各杆端弯矩为固端弯矩,其值计算如下:
Mba=0.125qL2=0.125q×142=24.5q.
Mbc=-0.0833qL2=-0.0833q×262=-56.33q.
Mcb=0.0833qL2=0.0833q×262=56.33q.
Mcd=-0.125qL2=-0.125q×142=-24.5q.
1.2.1.3 按力矩分配法原理进行力矩分配:
Mba=Mbc=Mcb=Mcd=47.88q1.2.1.4 计算支点反力.
(1)A 点支点反力 RA:14Ra+47.88 q-0.5qL2=0 Ra=3.58q.
(2)B 点支点反力 RB:40Ra+26Rb+47.88q-0.5qL2=0 Rb=23.42q.
同理计算 RC=23.42q,RD=3.58q.
根据支点反力和受力图绘如下贝雷梁的剪力图:
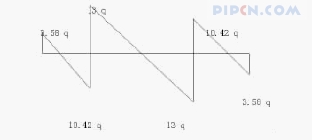
1.2.1.5 计算跨中挠度
(1)计算中跨跨中挠度
①计算外力作用下中跨跨中挠度
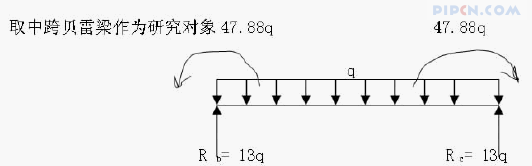
中跨贝雷梁受力如上图所示,因在一般情况下,梁的变形均极微小,且在材料的线弹性范围内,即梁的位移与荷载呈线性关系,由此可根据叠加原理计算其位移,即只需先分别计算出各项荷载单独作用时所引起的位移,再求出它们的代数和,即为梁上所有荷载作用下的总位移,下面按照叠加原理计算梁的跨中挠度。 中跨贝雷梁所承受的外力如上图,跨中挠度主要由支点负弯矩引起的上挠和均布荷载引起的下挠,跨中挠度为三者的叠加,具体计算如下(其中支点负弯矩引起的挠度按图乘法计算)
M=47.88q.
支点负弯矩作用的弯矩图

单位荷载作用下的弯矩图
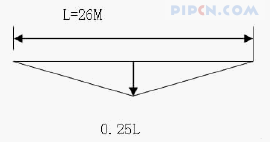
均布荷载作用下的弯矩图
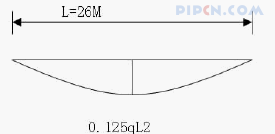
计算支点负弯矩作用下的跨中上挠挠度.
f 中=(0.5L×0.25L×47.88q)/EI=5.985L2q/EI=4046q/EI.
计算均布荷载作用下的跨中下挠挠度.
f 中=5qL4/384EI=5950.2q/EI.
将 E=2.1×1011Pa,4 片上下加强贝雷梁 I=4×577434×10-8m4则中跨跨中挠度为 f=(5950.2-4046)q/EI=3.93×10-5q(CM).
②计算因贝雷销间隙引起的非弹性挠度
f=0.05×0.1524(72-1)/2=1.83cm.
③中跨跨中挠度即为外力作用下的弹性挠度和非弹性挠度之和,具体计算如下:
f=3.9q×10-5+1.83.
1.2.2 边跨跨中挠度计算
1.2.2.1 外力作用下的弹性挠度计算
f=5qL4/384EI-3qL2/EI=(500-587)q/EI=-87q/EI.
1.2.2.2 计算因贝雷销间隙引起的非弹性挠度
f=0.5×0.1524(52-1)/2=0.91cm.
1.2.2.3 边跨跨中挠度即为外力作用下的弹性挠度和非弹性挠度之和,具体计算如下:
f 边=-1.8×10-6+0.91(CM).
1.2.3 贝雷片在自重作用下的挠度计算
1.2.3.1 4 片贝雷片的自重荷载 q=(270×4+80×2×4+21×3+3×3)/3=5973N/M
则中跨跨中挠度 f=3.9q×10-5+1.83=2.06cM.
f 边=-1.8 q×10-6+0.91=0.9CM.
1.2.3.2 当均布荷载为 1.6770n/m 时的挠度(采用贝雷片横铺叠放6 层)
fz=3.9q×10-5+1.83=2.48M.
f 边=-1.8×q10-6+0.91=0.88CM.
1.2.3.3 当均布荷载为 2.7570n/m 时的挠度 (采用贝雷片横铺叠放12 层)
fz =3.9q×10-5+1.83=2.9M.
f 边=-1.8×q 10-6+0.91=0.86CM.
1.3 采用水准仪测量贝雷梁实际挠度
2.试验结果整理
第一次挠度试验结果汇总(26 米跨跨中)
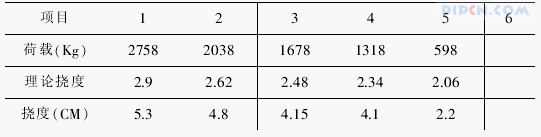
由上表实测数据,按弹性变形理论推算贝雷梁的负荷与挠度关系如下式:
f 中=0.00833q+30.
q___ 均布荷载,单位:Kg/m.
f 中——通航孔支点挠度;单位:cm.
第二次挠度试验结果

通过上述试验结果,可以得到:在跨河大桥支架的搭设,三跨贝雷梁支架支点宽度为 4M 时,理论计算挠度与实际挠度相差较小,且实际挠度比理论挠度值要小,可以用于贝雷梁的搭设。 来源: 《建筑中文网》.
跨河大桥跨采用整体现浇施工,由于桥跨跨越河流,施工时为尽量降低对河道通航的防碍,支架在中跨中间设净空 18 米×5 米的通航孔, 在通航孔两侧各设入土 12 米的 21 根 φ0.5 米的钢管桩作临时支点。 拟采用国产 321 公路钢桥桁架(国内通常称为贝雷架)架设连续梁支架,分别支承在桥跨的八个支点处。 为确定支架的实际挠度与理论计算挠度的相符性,需进行三跨连续贝雷梁进行试验。(参考《建筑中文网》)
1.贝雷梁试验
1.1 贝雷梁的假设
计划在桥头路面上布置同高的四个支点,跨度组合为 14+26+14,上搭设单层上下加强 4 排贝雷片,横向每隔 3 米上下采用钢管加固,在贝雷梁上分批采用贝雷片加载。 采用水准仪测其实际的挠度,并与理论计算值相比较。 为比较支点宽度对贝雷梁变形的影响,试验分两次进行,第一次支点宽度约 50CM,即接近点接触状态,第二次支点宽度为4 米,即完全模仿现浇箱梁支架。
1.2 贝雷梁挠度理论值计算
1.2.1 计算中跨 26 米、边跨 14 米连续梁的跨中挠度,计算模型如下

1.2.1.1 让算弯矩分配系数
(1)计算刚度系数(设 EI=26)
iba=EI/L=26/14=1.857 ibc=EI/L=26/14=1.857.
icb=EI/L=26/14=1.857 icd=EI/L=26/14=1.857.
(2)计算弯矩分配系数
在计算某一节点处的分配系数时,相邻的刚结点,应作为临时固端看待。
μba=3iba/(3iba+4ibc)=3×1.857/(3×1.857+4×1)=0.58.
μbc=4ibc/(3iba+4ibc)=4×1.857/(3×1.857+4×1)=0.42.
μcb=4icb/(3icd+4i)=4×1.857 /(3×1.857+4×1)=0.42.
μcd=3icd/(3icd+4icb)=3×1.857/(3×1.857+4×1)=0.58.
1.2.1.2 固端弯矩计算
在连续梁的 B、C 两支点加约束使其固定, 这时各杆端弯矩为固端弯矩,其值计算如下:
Mba=0.125qL2=0.125q×142=24.5q.
Mbc=-0.0833qL2=-0.0833q×262=-56.33q.
Mcb=0.0833qL2=0.0833q×262=56.33q.
Mcd=-0.125qL2=-0.125q×142=-24.5q.
1.2.1.3 按力矩分配法原理进行力矩分配:
Mba=Mbc=Mcb=Mcd=47.88q1.2.1.4 计算支点反力.
(1)A 点支点反力 RA:14Ra+47.88 q-0.5qL2=0 Ra=3.58q.
(2)B 点支点反力 RB:40Ra+26Rb+47.88q-0.5qL2=0 Rb=23.42q.
同理计算 RC=23.42q,RD=3.58q.
根据支点反力和受力图绘如下贝雷梁的剪力图:

1.2.1.5 计算跨中挠度
(1)计算中跨跨中挠度
①计算外力作用下中跨跨中挠度

中跨贝雷梁受力如上图所示,因在一般情况下,梁的变形均极微小,且在材料的线弹性范围内,即梁的位移与荷载呈线性关系,由此可根据叠加原理计算其位移,即只需先分别计算出各项荷载单独作用时所引起的位移,再求出它们的代数和,即为梁上所有荷载作用下的总位移,下面按照叠加原理计算梁的跨中挠度。 中跨贝雷梁所承受的外力如上图,跨中挠度主要由支点负弯矩引起的上挠和均布荷载引起的下挠,跨中挠度为三者的叠加,具体计算如下(其中支点负弯矩引起的挠度按图乘法计算)
M=47.88q.
支点负弯矩作用的弯矩图

单位荷载作用下的弯矩图

均布荷载作用下的弯矩图

计算支点负弯矩作用下的跨中上挠挠度.
f 中=(0.5L×0.25L×47.88q)/EI=5.985L2q/EI=4046q/EI.
计算均布荷载作用下的跨中下挠挠度.
f 中=5qL4/384EI=5950.2q/EI.
将 E=2.1×1011Pa,4 片上下加强贝雷梁 I=4×577434×10-8m4则中跨跨中挠度为 f=(5950.2-4046)q/EI=3.93×10-5q(CM).
②计算因贝雷销间隙引起的非弹性挠度
f=0.05×0.1524(72-1)/2=1.83cm.
③中跨跨中挠度即为外力作用下的弹性挠度和非弹性挠度之和,具体计算如下:
f=3.9q×10-5+1.83.
1.2.2 边跨跨中挠度计算
1.2.2.1 外力作用下的弹性挠度计算
f=5qL4/384EI-3qL2/EI=(500-587)q/EI=-87q/EI.
1.2.2.2 计算因贝雷销间隙引起的非弹性挠度
f=0.5×0.1524(52-1)/2=0.91cm.
1.2.2.3 边跨跨中挠度即为外力作用下的弹性挠度和非弹性挠度之和,具体计算如下:
f 边=-1.8×10-6+0.91(CM).
1.2.3 贝雷片在自重作用下的挠度计算
1.2.3.1 4 片贝雷片的自重荷载 q=(270×4+80×2×4+21×3+3×3)/3=5973N/M
则中跨跨中挠度 f=3.9q×10-5+1.83=2.06cM.
f 边=-1.8 q×10-6+0.91=0.9CM.
1.2.3.2 当均布荷载为 1.6770n/m 时的挠度(采用贝雷片横铺叠放6 层)
fz=3.9q×10-5+1.83=2.48M.
f 边=-1.8×q10-6+0.91=0.88CM.
1.2.3.3 当均布荷载为 2.7570n/m 时的挠度 (采用贝雷片横铺叠放12 层)
fz =3.9q×10-5+1.83=2.9M.
f 边=-1.8×q 10-6+0.91=0.86CM.
1.3 采用水准仪测量贝雷梁实际挠度
2.试验结果整理
第一次挠度试验结果汇总(26 米跨跨中)

由上表实测数据,按弹性变形理论推算贝雷梁的负荷与挠度关系如下式:
f 中=0.00833q+30.
q___ 均布荷载,单位:Kg/m.
f 中——通航孔支点挠度;单位:cm.
第二次挠度试验结果

通过上述试验结果,可以得到:在跨河大桥支架的搭设,三跨贝雷梁支架支点宽度为 4M 时,理论计算挠度与实际挠度相差较小,且实际挠度比理论挠度值要小,可以用于贝雷梁的搭设。 来源: 《建筑中文网》.
原文网址:http://www.pipcn.com/research/201011/14483.htm
也许您还喜欢阅读:
