碳纤维、钢纤维混凝土低周抗压疲劳特性的试验研究
- 椰子废弃物资源综合利用问题与对策
- 塔式起重机的使用与安全管理
- 无机保温材料在建筑外墙保温系统的应用
- 城市生态环境保护与绿色建筑材料
- 建筑材料的质量检测问题和防治措施
- 钢结构建筑的发展现状和应用前景
- 绿色建材与建筑节能
- 钢结构在民用建筑上应用价值、发展重点和难点
- 解决城市交通拥堵和停车难的途径:机械式停车
- 广州珠江新城西塔高空重型塔式起重机拆除技术
内容提示:本文研究了素混凝土、碳纤维混凝土和钢纤维混凝土在轴压疲劳荷载下的破坏机理,试验研究了碳纤维、不同品种钢纤维、纤维掺量、加载应力水平对于疲劳寿命及能量吸收的影响规律,探讨了疲劳累积损伤特性。研究表明在较低的应力水平下纤维混凝土的疲劳寿命、能量吸收值均比高应力水平时明显增大。
近几年来,纤维混凝土已广泛应用于对抗疲劳、抗震和抗冲击等有较高要求的土木工程领域,这些工程在其服役期内通常承受随机或周期性反复荷载的作用,因此,研究纤维混凝土在不同加载应力水平下的疲劳寿命、能量吸收和疲劳累积损伤特性是极其重要的,它是建立纤维混凝土疲劳累积损伤理论和正确估算结构剩余疲劳寿命等工作的基础。过去关于素混凝土及钢纤维混凝土疲劳特性的研究较多[1~4],但关于碳纤维混凝土疲劳特性的研究未见报道。本文对碳纤维和钢纤维增强混凝土的疲劳特性作了对比试验,重点研究了碳纤维掺量、加载应力水平对疲劳寿命、能量吸收值及疲劳累积损伤变量的影响规律。研究表明:钢纤维和碳纤维混凝土均具有良好的抗疲劳特性,钢纤维混凝土的疲劳寿命是素混凝土的7.9~13.7倍,能量吸收是素混凝土7.4~14.5倍,碳纤维混凝土的疲劳寿命是素混凝土2.1~9.3倍,能量吸收是素混凝土1.53~4.2倍;与高应力水平相比,纤维混凝土在较低应力水平下的疲劳寿命、能量吸收均有明显增大的趋势。(参考《建筑中文网》)
1 试验过程
表1 纤维混凝土力学性能
| | |||
| 试件编号 | 纤维体积率(%) | 轴心抗压强度/MPa | 弹性模量/GPa |
| | |||
| C | 0.00 | 20.8 | 14.96 |
| CF1 | 0.10 | 21.0 | 12.43 |
| CF2 | 0.20 | 21.9 | 12.97 |
| CF3 | 0.25 | 22.5 | 13.42 |
| SE | 1.0 | 20.9 | 20.10 |
| SK1 | 1.2 | 21.1 | 22.40 |
| SK2 | 1.6 | 22.9 | 23.71 |
| SK3 | 2.0 | 23.4 | 24.01 |
| | |||
1.1 试件 试验所用材料及混凝土配合比见文献[5]。棱柱体试件尺寸为100mm×100mm×300mm,各类试件个数均为6个,纤维混凝土力学性能列于表1,表中C代表素混凝土,CF1~CF3代表碳纤维混凝土,SE代表E型钢纤维混凝土,SK1~SK3代表K型钢纤维混凝土。
1.2 静载试验 在作疲劳试验前先作了静载抗压试验,以确定试件破坏时的最大荷载。试件室内自然养护45d后作试验。由于试件数量较多,试验持续时间达9d,为了取得较精确的静载轴心抗压强度,用以下方法来测算疲劳试验时任意一天的轴心抗压强度,并以此来确定疲劳试验中的应力水平。
试验开始的当天,测一组试件的轴心抗压强度,试验过程中每隔3d测一组轴心抗压强度,代入下式[4]确定A、B常数。
| fc,t=Alogt+B | (1) |
式中:fc,t为龄期t天时的轴心抗压强度。利用式(1)可求得任意给定一天的轴心抗压强度。
1.3 疲劳试验装置及试验过程 整个试验在德国生产的电液伺服系统试验机上完成,疲劳加载按恒力控制,加载波为正弦波,频率为0.5Hz.为了避免加载过程中出现非接触情况,试件上保持了0.05Fmax的最小压力(Fmax为静载试验时的最大荷载).测试系统由试验机自带的位移计、压力传感器、动态应变仪和x-y函数记录仪组成,同时用计算机自动采集系统记录和显示数据。记录仪记录了疲劳过程中的荷载-位移曲线。加载应力水平τ等于疲劳荷载与静载轴心抗压强度的比值,本试验τ分别取0.70、0.80、0.90和0.95.
2 试验结果及分析
2.1 疲劳试验结果
2.1.1 疲劳寿命 素混凝土、碳纤维及钢纤维混凝土在4种不同应力水平下的疲劳寿命列于表2.
表2 纤维混凝土抗压疲劳寿命
| | |||||||||
| 试 件 | |||||||||
| τ | | ||||||||
| C | CF1 | CF2 | CF3 | SE | SK1 | SK2 | SK3 | ||
| | |||||||||
| 0.70 | 平均值 | 191 | 1600 | 1788 | 1874 | 2270 | 2393 | 2421 | 2625 |
| 变异性δ | 0.15 | 0.08 | 0.09 | 0.07 | 0.10 | 0.09 | 0.08 | 0.08 | |
| 0.80 | 平均值 | 79 | 258 | 333 | 342 | 562 | 634 | 734 | 777 |
| 变异性δ | 0.15 | 0.01 | 0.07 | 0.11 | 0.19 | 0.03 | 0.11 | 0.08 | |
| 0.90 | 平均值 | 31 | 88 | 103 | 117 | 187 | 192 | 200 | 179 |
| 变异性δ | 0.22 | 0.13 | 0.12 | 0.15 | 0.12 | 0.11 | 0.11 | 0.14 | |
| 0.95 | 平均值 | 13 | 19 | 24 | 27 | 103 | 115 | 121 | 124 |
| 变异性δ | 0.21 | 0.20 | 0.21 | 0.20 | 0.24 | 0.10 | 0.18 | 0.24 | |
| | |||||||||
由表2可见,随着加载应力水平的提高,纤维混凝土的疲劳寿命减少,纤维体积率增加时,疲劳寿命增大。钢纤维混凝土的疲劳寿命是碳纤维混凝土的1.6~6.5倍。试件SE与SK1中纤维体积率接近,两种钢纤维均能均匀地分布于混凝土中,施工性良好。但是,带钩的K型钢丝纤维的疲劳寿命高于E型剪切类钢纤维。
在较低应力水平下,纤维混凝土的疲劳寿命高,但当τ≥0.80时,疲劳寿命明显降低。试验时清晰地观察到:当应力水平较低时(如图1(a)所示),在循环初期,试件表面的可视裂纹少而短,循环次数增加,已有裂纹不再继续增长或增长十分缓慢,随着循环次数的进一步增加,新生疲劳裂纹不断萌生和扩展,最后,已有裂纹与新生裂纹共同向前扩展,并相互贯通,形成一条通缝,导致试件破坏。从试件内部损伤机制看,在低应力水平下,疲劳裂纹端部的应力集度小于纤维的阻力,纤维阻止了裂纹的扩展,要使裂纹通过钢纤维或高强碳纤维,就需增加循环次数,促使疲劳裂纹的扩展与贯通。在较高应力水平,如τ≥0.80时,循环初期,试件表面可视裂纹多而粗,当循环次数增加时,已有裂纹不断扩展,新裂纹逐渐萌生和扩展,最后两种裂纹在疲劳荷载作用下,相互搭接和贯通,导致试件破坏(如图1(b)所示).从试件内部损伤机制看,较高应力水平下,混凝土基体中裂纹端部的应力集度大于纤维的阻力,裂纹进一步扩展,累积损伤增大,疲劳寿命减少。
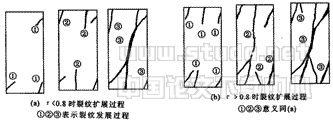
图1 疲劳裂纹扩展过程示意
碳纤维混凝土疲劳寿命与应力水平、纤维体积率的关系如图2所示,图中纵坐标为碳纤维混凝土疲劳寿命与素混凝土的比值。在不同的应力水平下,碳纤维对混凝土疲劳寿命的提高幅度不同。但是,随着碳纤维体积率的增大,碳纤维混凝土的疲劳寿命基本上按线性规律增加,即
| Ncf/Nc=a+bνcf | (2) |
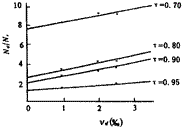 |
| 图2 碳纤维混凝土相对疲劳寿命与纤维体积率的关系曲线 |
式中:νcf为碳纤维体积率,单位为(‰),下同;Ncf为碳纤维混凝土的疲劳寿命;Nc为素混凝土的疲劳寿命。应力水平不同,则a、b系数不同。当τ=0.70时,a=7.62,b=0.78;τ=0.80时,a=2.40,b=0.80;τ=0.90时,a=1.98,b=0.73;τ=0.95时,a=1.21,b=0.33.这表明碳纤维混凝土的疲劳寿命与应力水平密切相关,当应力水平τ由0.70升为0.80时,碳纤维混凝土疲劳寿命与素混凝土疲劳寿命的比值明显减小。
2.1.2 能量吸收 试件在疲劳荷载作用下荷载-位移曲线下的面积为其所吸收的能量值,用J表示。当试件破坏时,荷载-位移曲线下的面积为疲劳过程中所吸收的总能量,用Jtot表示,总能量吸收值列于表3.
表3 纤维混凝土所吸收的总能量(单位:N·m)
| 试 件 | |||||||||
| τ | | ||||||||
| C | CF1 | CF2 | CF3 | SE | SK1 | SK2 | SK3 | ||
| 0.70 | 平均值 | 1273 | 4758 | 5081 | 5326 | 12793 | 14837 | 16069 | 18416 |
| 变异性δ | 0.07 | 0.04 | 0.03 | 0.02 | 0.08 | 0.04 | 0.03 | 0.034 | |
| 0.80 | 平均值 | 709 | 1454 | 1503 | 1609 | 3653 | 4489 | 5488 | 5637 |
| 变异性δ | 0.03 | 0.06 | 0.10 | 0.03 | 0.16 | 0.05 | 0.06 | 0.06 | |
| 0.90 | 平均值 | 393 | 603 | 804 | 919 | 2002 | 2325 | 2372 | 3221 |
| 变异性δ | 0.14 | 0.12 | 0.17 | 0.08 | 0.05 | 0.14 | 0.12 | 0.06 | |
| 0.95 | 平均值 | 224 | 344 | 367 | 392 | 1200 | 1461 | 1657 | 1658 |
| 变异性δ | 0.17 | 0.15 | 0.11 | 0.13 | 0.06 | 0.23 | 0.18 | 0.09 | |
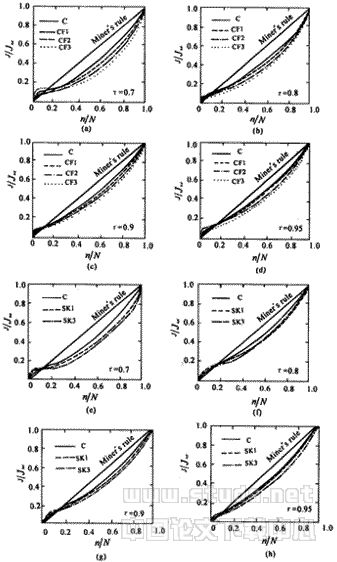
图3 纤维混凝土能量吸收比与循环比的关系曲线
纤维混凝土试件在疲劳过程中裂纹扩展、纤维的脱粘与拔出等都需吸收能量,总的能量吸收与疲劳寿命、纤维体积率、应力水平以及损伤发展密切相关。与高应力水平相比,在较低的应力水平下,疲劳裂纹短而且少,纤维与基体间有良好的粘结力,纤维延缓了裂纹的扩展,增大了基体的疲劳寿命、可恢复变形和能量吸收值,试件能吸收更多的能量。当应力水平提高时,砂浆体中产生更多的裂纹,消弱了纤维对裂纹的阻滞作用,裂纹扩展速率和不可逆变形增大,疲劳寿命和能量吸收值减少。钢纤维与碳纤维的弹性模量接近,但钢纤维混凝土在疲劳过程中吸收的能量值大于碳纤维混凝土,这是由于钢纤维两端带钩,增加了钢纤维与基体间的摩擦力,在钢纤维被拔出的过程中即钢纤维混凝土的破坏阶段所吸收的能量大于碳纤维混凝土。钢纤维更有利于提高混凝土的耗能性能。
2.2 疲劳累积损伤规律
试件内部的损伤演化与能量吸收密切相关。从能量吸收的角度定义损伤变量D为:
| D=J/Jtot | (3) |
图3为试件能量吸收相对值或损伤变量D与循环次数比的关系曲线。由图可见,纤维混凝土的累积损伤为非线性损伤,用Miner线性损伤准则计算纤维混凝土结构的剩余寿命偏于保守,加载应力水平对于能量吸收或损伤演化有影响。纤维混凝土材料的能量吸收或累积损伤发展大致分为三个阶段:第一阶段,循环初期,n/N≤0.15时,能量吸收较快,由于材料的弹性变形在吸收能量,但损伤变形发展较慢,因此该阶段用能量吸收值来估算累积损伤不够准确;第二阶段,0.2≤n/N≤0.85,材料处于能量吸收或损伤演化的稳定发展阶段,能量吸收或累积损伤与循环次数基本呈线性增长规律,试件所吸收的能量用于裂纹萌生、稳定扩展和纤维的脱粘等,能量吸收反映了累积损伤发展规律;第三阶段,n/N>0.85,处于能量吸收或累积损伤的快速发展阶段,试件中的裂纹由稳定扩展变为非稳定扩展,裂纹扩展速率加快,纤维不断被拔出,当纤维被拔出后,试件完全丧失承载力。
图3中,纤维混凝土的累积损伤发展与应力水平及纤维掺量有关,经统计分析得到碳纤维混凝土累积损伤变量Dcf以及钢纤维混凝土累积损伤变量Ds分别为:
| Dcf= J/Jtot=(n/N)1-(3.1+1.7νcf)log(0.9τ) | (4) |
| Ds= J/Jtot=(n/N)1-(3.1+2.4νsfl/d)log(0.9τ) | (5) |
式中:τ为应力水平,τ≥0.70;n/N为循环比。
3 结 论
(1)在对纤维混凝土进行疲劳设计和疲劳强度分析时,应考虑应力水平对疲劳寿命及能量吸收的影响。纤维混凝土在较低应力水平下的疲劳寿命和能量吸收比高应力水平时有明显的增大趋势。当应力水平大于或等于破坏荷载的80%时,纤维混凝土的疲劳寿命和能量吸收明显降低;纤维在较低应力水平下表现出很强的阻滞作用,延缓了混凝土基体的损伤发展。(2)当钢纤维体积率为1.0%~2.0%,碳纤维体积率为1.0‰~2.5‰时,钢纤维混凝土的疲劳寿命是碳纤维混凝土的1.6~6.5倍,能量吸收是碳纤维混凝土的3.9~4.8倍。(3)试件在疲劳过程中所吸收能量的相对值,较真实地反映了钢纤维和碳纤维混凝土的非线性疲劳累积损伤过程,用Miner线性累积损伤理论计算纤维混凝土的疲劳累积损伤偏于保守。
参 考 文 献:
[1] Byong Y B,Cheng-Tzu T H.Properties of Steel Fiber Reinforced Concrete under Cyclic Loading[J]。ACI Materials J.,1998,95(2).
[2] Hsu T C.Fatigue and Microcracking of Concrete[J]。RILEM,Materials and Structures,1984,17(97).
[3] 孙伟,高建明。路用钢纤维混凝土抗折疲劳特性研究[J]。东南大学学报,1993,21(2).
[4] 鞠杨,樊承谋。钢纤维混凝土轴压疲劳性能研究[A]。第五届全国纤维水泥与纤维混凝土学术会议 来源: 《建筑中文网》.
原文网址:http://www.pipcn.com/research/200602/8327.htm
也许您还喜欢阅读:
