利用离散小波探测沉降测值异常
- 改进的隧道监测系统(TMS)在隧道围岩变形监测中的应用
- 我国岩土工程在可持续发展中的新使命及其实现问题
- 矿山地质环境治理问题研究
- 岩土工程勘察中常见的技术问题及解决措施探讨
- RTK-GPS在广州新电视塔变形监测中的应用研究
- 既有建筑物加固修缮勘察与地基基础加固方案选择
- 现场测量建筑围护结构节能特性的问题分析
- 文物保护建筑勘察特点及工程实例分析
- 旁侧荷载对复合地基性状的影响
- 从工程实例分析谈顺层岩质边坡的勘察与参数选取
内容提示:研究小波变换在沉降测值异常探测中的应用问题,实例分析证明借助离散小波的多分辨率分析,能有效地探测和剔除沉降观测中的异常值,获得有效的沉降数据,为进一步进行沉降分析与预报提供可靠保证。 【
【摘 要】研究小波变换在沉降测值异常探测中的应用问题,实例分析证明:借助离散小波的多分辨率分析,能有效地探测和剔除沉降观测中的异常值,获得有效的沉降数据,为进一步进行沉降分析与预报提供可靠保证。(参考《建筑中文网》)
【关键词】小波变换;多分辨率分析;异常值
1 引言
大型建筑物沉降观测中,沉降异常包含两方面内容:一是由于观测过程中各种复杂因素的影响或数据传递、加工过程中的差错,导致观测值存在不规则的粗差;二是由于建筑物的显著沉降,使观测值产生突变的现象。无论沉降异常是属于粗差还是突变,在建立沉降观测模型之前,都应当进行准确的探测和分析,否则将导致沉降分析和预报上的偏差。
大型建筑物沉降观测的周期一般较长,观测频次较多,大量的沉降信息相当于一组非平稳信号,沉降异常值可以看成是这组信号中的奇异点,而小波分析在探测这些反常现象并展示其成分方面有其独特的一面。本文先对小波及其变换方法进行论述,然后结合城市地铁沉降观测实例进行计算和分析。
2 小波基本理论
2·1 小波及其变换
设Ψ(x)∈L2(R),(L2(R)(表示平方可积的实数空间),其傅里叶变换为Ψ(ω),当Ψ(ω)满足下述条件:
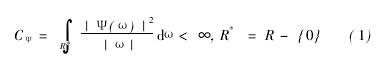
时,Ψ(ω)称为小波母函数。
小波实际上是由小波母函数Ψ(x)以一定的尺度即伸缩因子a和平移因子b进行伸缩与平移得到的函数序列
{Ψa,b(x)},设Ψ(x)∈L2(R),母函数Ψ(x)经伸缩和平移后得[1]
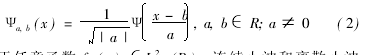
对于任意函数f(x)∈L2(R),连续小波和离散小波分别可变换为式(3)、(4),即
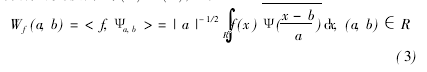
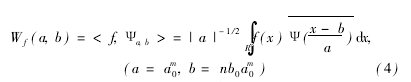
上式中a0>1,b0>0,m,n∈z。常取a0=2,b0=1称为二进制小波函数。
实际应用中,尤其是在计算机上实现时,连续小波必须加以离散化,即离散小波。
2·2 多分辨率分析
空间L2(R)中的多分辨率分析是指L2(R)中满足单调性、逼近性、伸缩性、平移不变性、Riesz基存在性等条件(此处省略具体描述)的一个空间序列{Vk}[2]。多分辨率分析可以将被处理的信号用正交变换在不同的分辨级上进行分解。

小波变换利用多分辨率分析将信号分为不同频段(高频和低频),趋势成分保留在低频部分中。若原始采样信号中含有瞬变成分,经过有限次变换后信号的高频部分会出现迅变,从而发现原始信号中的异常现象。沉降观测中可以利用这一优点来探测异常值。
3 基于小波的异常探测
3·1 信号奇异性检测

对于某一特定尺度s,Wf(s,t)沿时间t的极大值对应了f*θ(t)的突变点。θ(t)是可微的,若θ(t)的等效宽度足够小,则Wf(s,t)的极值点的位置应出现在f(t)的模极大值附近,也就是说,由小波变换的模极大值点可以找到原始信号中的突变点。
沉降观测序列可以看作随时间或空间变化的信号,信号中的奇异点及不规则的突变部分可以看做是异常值。利用小波分析进行异常探测的基本方法是:对沉降观测序列进行多尺度分析,在信号发生突变时,其小波变换后的系数具有模极大值,由此可以检测出观测时间序列的异常值。小波分析探测方法只是根据效应量的序列本身之间的内在联系进行检验,并未涉及效应量的成因,实际应用中,应该利用数学模型对这些异常值进行检验,若实测值与拟合值之间的残差未超过±3σ(σ为标准差),则说明这些观测值属于环境因素显著变化引起的正常值,否则属于粗差。
3·2 利用小波消噪进行异常值探测
小波消噪即是在不同尺度下作小波变换,其实质就是用不同中心频率的带通滤波器对信号进行滤波,把那些主要反映噪声频率的尺度小的小波变换去掉,即可得到质量较好的有用信号。
一个含噪声的一维信号的模型可以表示成如下的形式:
s(i)=f(i) σe(i) i=0,…,n-1(8)
其中,f(i)为真实信号,e(i)为噪声,s(i)为含噪声的信号,σ为模型的标准偏差。
实际工程中,有用信号通常表现为低频信号或是一些比较平稳的信号,而噪声信号则通常表现为高频信号,所以消噪过程可以按如下方法进行处理:首先对信号进行小波分解,再以阈值等形式对小波系数进行处理,然后对信号进行重构,即可得到消噪后的观测数据序列估计值。
以城市地铁某段多期沉降观测数据为例,说明应用离散小波进行测值异常探测的过程及其有效性。以某点的86期观测成果为探测对象,利用db3小波[3]对数据进行三层小波分解,图1为小波分解过程图。
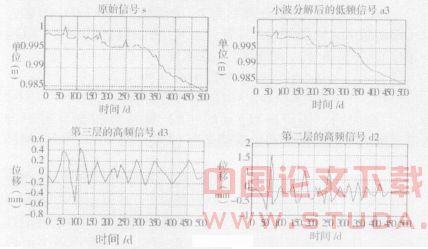
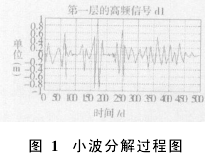
其中s为沉降时间序列,d1、d2、d3对应着小波分解后第一层、第二层、第三层的高频部分,a3对应着第三层的低频部分。由图1可以看出,第一层和第二层的高频部分分别在t=62、t=170、t=249有模极大值点,可能为观测序列的异常值。分别对三个时刻对应的值进行检验,对应的实测值与拟合值之间的残差均大于三倍标准差,所以均是异常值。另外,在第一层上还有一些数量较多、幅值不大的模极值点,其奇异性主要是由随机噪声(随机误差)引起,但对应的实测值与拟合值之间的残差均小于三倍标准差。
找到异常值所在后,再进行小波分解高频系数的阈值消噪处理。对第1层到第3层的每一层高频系数,选择一个阈值进行软阈值量化处理。本文采用三种方法进行小波阈值消噪,其中,强制消噪处理是把小波分解结构中的高频系数全部变为0,即把高频部分全部滤除掉,然后再对信号进行重构处理;默认阈值消噪处理是利用Matlab中ddencmp函数[4]产生信号的默认阈值,然后利用wdencmp函数进行消噪处理;给定软(或硬)阈值消噪处理是根据经验选取阈值进行消噪处理。经过阈值软化,用小波分解后的最后一层低频系数和经过阈值消噪处理后的各层高频系数进行重构,得到消噪后的观测数据序列估计值。小波消噪后的波形图如图2所示。
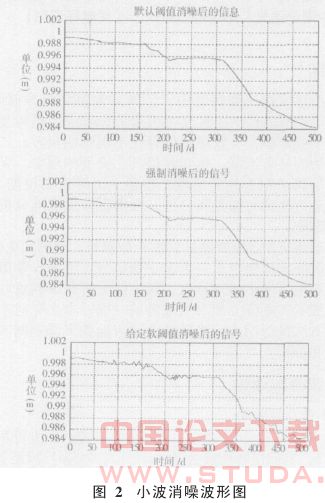
在给定软阈值消噪处理过程中,三层给定的阈值均为0,由图2可以看出,曲线消噪后比消噪前光滑得多,这说明在一定程度上消除了噪声,但由于小波的选择、阈值处理、分解层数的确定没有优化,因此还存在一些弱噪声,这也是作者将进一步研究的内容。
5 结束语
本文在学习小波理论和分析方法的基础上,结合城市地铁某段多期沉降观测数据进行分析,研究表明:利用小波多分辨率分析功能,能较好的探测和剔除变形监测工程中观测序列的异常值,使变形分析和变形预报更准确可靠。
参考文献
[1]程正兴·小波分析算法与应用[M].西安:西安交通大学出版社,1998·
[2]冉启文·小波分析与分数傅立叶变换及应用[M].北京:国防工业出版社,2002·
[3]陈继光,李光东,刘中波·大坝变形数据处理中的离散小波分析方法[J].水电能源科学,2003,(4)·
[4]何仁斌·Matlab6工程计算与应用[M].重庆:重庆大学出版社,2001·
原文网址:http://www.pipcn.com/research/200810/8961.htm
也许您还喜欢阅读:
