地铁控制基标的归化改正原理和编程实现
- 工程爆破行业的信息化发展现状、实施问题和建议
- BIM技术及在工程项目管理模式中的应用
- 建筑扬尘污染监控平台中的Kerberos协议改进
- 云计算安全研究参考文献
- 云计算安全研究报告(5):云计算安全关键技术研究
- 云计算安全研究报告(4):云计算安全技术框架建议
- 云计算安全研究报告(3):云计算安全现状
- 云计算安全研究报告(2):云计算安全挑战
- 云计算安全研究报告(1):云计算发展趋势
- 大型集团型建筑企业工程管理信息化工作探索
内容提示:介绍控制基标在地铁建设中的作用和测设步骤,总结铺轨基标归化改正计算的理论依据和基本方法,建立了数学模型;同时在VB6.0环境下编程实现了归化改正点位的自动判定和改正值的自动计算。最后给出编程原理、流程图和工程实例。
[摘要]介绍控制基标在地铁建设中的作用和测设步骤,总结铺轨基标归化改正计算的理论依据和基本方法,建立了数学模型;同时在VB6.0环境下编程实现了归化改正点位的自动判定和改正值的自动计算。最后给出编程原理、流程图和工程实例。(参考《建筑中文网》)
[关键词] 地铁 控制基标 归化改正
1.铺轨基标在地铁工程中的地位和作用
铺轨基标是高标准轨道混凝土整体道床的轨道铺设控制点,精确地测设铺轨基标是保证轨道施工质量的关键。近年来,我国迅速发展的地铁、轻轨交通,对列车安全行驶的要求越来越高,这就对铺轨精度提出了更严格要求,因此精确测设铺轨基标是保证地铁轨道高精度施工的重要环节。
铺轨基标沿线路布设成导线形式,按精度等级可划分为控制基标和加密基标,测设时先测设控制基标,然后,利用控制基标测设加密基标。铺轨基标埋设位置有两种,即位于线路中线或线路中线的一侧。铺轨基标测量的实质是按照设计线路和铺轨综合设计图的要求,以一定的间隔,在线路中线或其一侧测设具有精确平面坐标和高程的标志,作为铺轨的平面和高程依据。
2.控制基标测设的一般步骤
控制基标的三维坐标在测设之前由测绘工程师根据铺轨综合设计图计算得出,测设控制基标大致分为三个步骤:
(1)初测:按三维坐标把控制基标放样到实地。
(2)调线测量:以附合导线形式串测控制基标,检测相邻控制基标间的夹角与距离是否满足规范限差要求。
(3)归化改正:根据调线测量成果计算控制基标间各夹角与理论值的较差,如有超限,则对部分或全部控制基标点位进行归化改正,使各控制基标间的几何关系满足限差要求。控制基标间高差关系一般好控制,在此不赘述。
3. 归化改正的一般方法和存在的问题
3.1一般方法:
(1)坐标法:根据调线测量平差结果,计算各控制基标坐标改正数(Vx,Vy),分别改正。
(2)角度距离法:根据控制基标串测导线的角度、距离偏差,沿线路垂直方向调整控制基标点位,使相邻控制基标的夹角满足限差要求。
上述方法中坐标法能严格将点位改正到理论位置,但计算烦琐,实地操作较困难,一般不被采用。而角度距离法在满足施工需要的前提下,合理忽略距离偏差,重点考虑角度偏差,计算、操作相对简单,在工程中得到普遍应用。
3.2存在问题:
通常进行角度距离法归化改正时,人为判断和选取需改正的点位,凭借经验试探该点横向改正值。由于在串测的导线上,一点的横向改正会引起相临两点间夹角的变化,因此须反复试探调整各点改正值,才能满足调线和归化改正要求。此方法既无固定规律又不严密,效率又低,实践经验不足的测量工作者很难掌握。
4. 归化改正计算程序的编程思想和特点
笔者针对上述归化改正中存在问题,在VB6.0下开发了控制基标归化改正计算程序,并在北京地铁、伊朗德黑兰地铁控制基标测量中得到了验证和应用。实践表明,该程序计算结果完全能够满足现行规范精度要求,解决了长期困扰测量工作者的难题。
4.1 编程思想:以角度距离法为出发点,总结点位横向改正值与角度改正数的变动规律,建立较合理的数学模型,寻求简洁实用的计算方法,实现归化改正点位自动选取与对应改正值的自动计算。
4.2 特点 :(1)计算快捷,直观。
(2)结果准确,满足施工精度要求。
(3)参数可自由设置,灵活实用。剩余夹角改正数限差、点属性[注1] 可由用户设置,可强制调整指定点的改正值。不受线路形状、基标布设形式限制。
5. 归化改正原理和数学模型
图一是控制基标以附合导线形式串测示意图,附合导线点数为n 3,边数为n 2,其中虚线表示控制基标串测附合导线理论位置,实线表示平差后的附合导线。
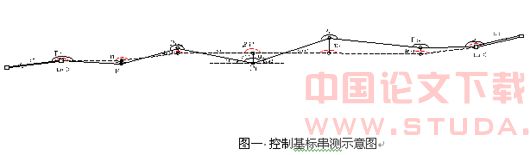
图一 控制基标串测示意图
图一中各符号的意义为:
Pi:第i个导线点(控制基标)的点名。
Si:第i-1点到第i 点的距离(观测值与理论值相差微小,以观测值表示)。
α0、αn:附合导线两端的已知方位角。
β’i:第i个控制点上的转折角理论值;βi:第i个转折角平差后的观测值。
ui:第i点沿线路法线方向的归化改正数,含正负号。正值表示向观测角一侧改正。
vi:转折角改正数,vi =β’i -βi;
5.1 归化改正原理:
已知转折角改正数vi(i=0,1,2…n)和观测边si(i =1,2…n),在Vi剩=0(Vi剩 为转折角改正数残差;i=0,1,2…n)或S (vi剩^2)=min(最小)的条件下,求各归化改正数ui(i =0,1,2…n)。
5.2数学模型的建立:


为求得U,下面讨论④式解的情况:
考察④式的系数矩阵B的秩有:
R(B)<=(n-1)<n 1,知B不可逆,方程④不是唯一解;
当R(B|U)=R(B),相容方程④有解,且有无穷多解。
当R(B|U)≠R(B),矛盾方程④无解。
针对以上两种情形,为求得④式的最优解,引入工程数学的“广义逆”(g逆)概念。设B的广义逆矩阵为B▔,最小范数g逆为Bm▔,最小二乘g逆为Bl▔;B的Moore-Penrose广义逆为B 。则
(1)当R(B|U)=R(B)<n 1时,相容方程④的最小范数解不唯一,它的一个解为
U=(1/ρ)Bm▔V ⑤
此时,U结果唯一,且满足 ||U||(U的范数)=最小。亦即横向归化改正值的平方和最小。
对于等边导线,设S1=S2=…=Sn=S,q=1/S 则④式中的B可写为:



此外等边导线具有两个重要规律:即满足两个公式(③和③’)。③’为等边导线所特有,也可用于检验等边导线观测值是否含有粗差。③是所有导线具有的规律,归化改正数的残差向量也符合这一规律,所以③除能检验观测值是否含有粗差外,还可以检验归化改正结果是否正确。
(2)当R(B|U) ≠R(B)时,矛盾方程④无解,但可求最优近似解,即最小二乘解(不唯一),其一个解为
U=(1/ρ)Bl▔V ⑥
⑥可使方程④残差向量的范数最小,即||ρBU||=最小。也就是附合导线的转折角改正数的残差向量的平方和为最小。
综合(1)、(2)两种情况,即无论方程④有解或无解,均可得到最优解,并可统一写为下式:
U=(1/ρ)B V ⑦
在(1)的情形下,⑦是④的一个最小范数解;在(2)情形下,⑦是④唯一的最小二乘最小范数解。
④、⑤、⑥三式或④、⑦二式即为控制基标归化改正的数学模型。
不论对于Bm-、Bl-还是B ,求解均有两种基本方法:满秩分解法、初等变换法。但精确解算十分繁琐,编程较难实现。实际编程是将V的残差向量(即转折角剩余改正数)的所有分量归化改正到满足限差要求为止。实践表明,该法可达到秒级精度要求。
6.程序流程图
程序流程图见图二
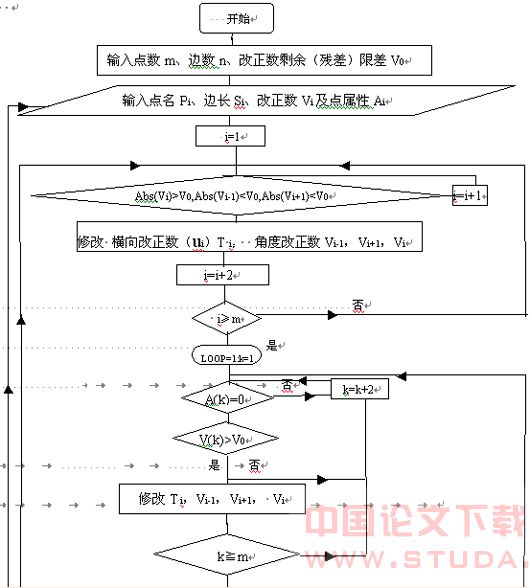
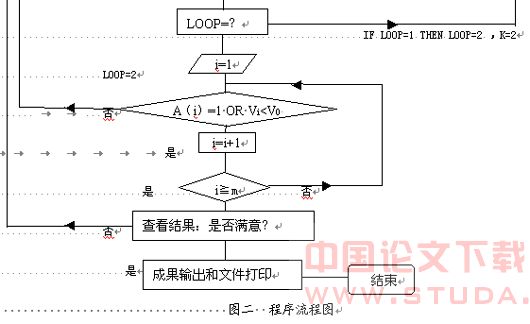
图二 程序流程图
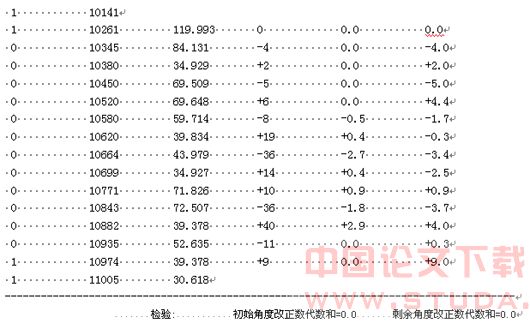
6. 工程实例
本例点数包括两端4个固定点共16个,边数包括两条起算边共15条。用程序按5”限差计算,
其中,折角改正数由转折角理论值减去观测值得到。计算成果见表一。
表一:归化改正计算成果表
7. 结束语
该控制基标归化改正程序,经过多年在北京、伊朗德黑兰地铁基标测量工程中使用,不仅可满足现行规范和施工要求,而且提高了工程效率和质量。归化改正程序必将在今后城市地下铁道、轻轨交通工程的铺轨基标工作中发挥其应有作用。同时,本归化改正程序对精密线形工程的高精度放样,也有一定的实用和参考价值。
[注1]点属性:1表示固定点;0表示未知点(参与归化改正计算)。
[注2]变换方法为:从第1行起,后两行加到前一行,依次类推到倒数第3行;再从倒数第2行起,每行加后边一行,依次类推至第1行。
参考文献:
[1] 秦长利。地铁铺轨基标测量方法探讨。铁路航测,1999(3)[2]北京城建勘察测绘院.《地下铁道、轻轨交通工程测量规范》(GB50308-1999).中国计划出版社, 2000年5月第一版[3] 陈永奇.《工程测量学》. 测绘出版社, 1995年5月第二版[4]於宗寿 鲁林成。《测量平差》。测绘出版社,1983年6月第二版
原文网址:http://www.pipcn.com/research/200808/8875.htm
也许您还喜欢阅读:
