请告诉我们您的知识需求以及对本站的评价与建议。
满意 不满意
Email:
基于振动模型的精密工作台运动控制
栏目最新
- 东莞至惠州城际铁路隧道安全风险评估与管理
- 高层建筑给排水系统安装施工技术
- 高层建筑施工质量的五个控制要点
- 房屋建筑工程质量问题、原因和防止措施
- 地下停车场防水工程施工质量预控措施
- 试析绿色施工技术在建筑工程中的应用
- 施工企业预算管理措施及案例分析
- 岩溶地区隧道施工综合预报技术案例分析
- 预制块镶面现浇混凝土隧道洞门施工方法
- 建筑施工模板应用技术简析
网站最新
内容提示：精密工作台高加减速的运动反力作用于机台上,会引起机台机械共振,使轨迹跟踪精度降低、定位建立时间加长,针对这一问题,提出了基于精密工作台振动模型,采用极点配置、模型参数匹配的方法设计PID控制器。通过实验,与PD 加速度前馈的控制方式相比较,当工作台以120mms、1g的加减速运动时工作台轨迹跟踪精度提高了2μm,定位建立时间缩短了10ms。结果表明,采用基于振动模型设计的PID运动控制具有
摘 要:精密工作台高加减速的运动反力作用于机台上,会引起机台机械共振,使轨迹跟踪精度降低、定位建立时间加长,针对这一问题,提出了基于精密工作台振动模型,采用极点配置、模型参数匹配的方法设计PID控制器。通过实验,与PD 加速度前馈的控制方式相比较,当工作台以120mm/s、1g的加减速运动时工作台轨迹跟踪精度提高了2μm,定位建立时间缩短了10ms。结果表明,采用基于振动模型设计的PID运动控制具有较好的动态响应和轨迹跟踪性能。（参考《建筑中文网》）
关键词:PID控制;直线电机;机械共振;精密工作台;极点配置
用于半导体制造装备或者精密加工的精密工作台,为了隔离外部振动,通常都安装在精密隔震台上,由于受结构限制,精密工作台的机台质量以及它的联结刚度就受到限制。在高速高加减速运动过程中,由于运动反力的作用,机台会产生机械共振[13],同时由于采用直线电机 气浮导轨的直接驱动形式,运动方向无机械阻尼,运动精度很容易受到机台共振的影响,使轨迹跟踪精度降低、定位建立时间加长。抑制机台的机械共振,可以通过附加阻尼装置或者反力引出装置[4,5]来实现,但是由于受环境制约,这些装置有时难于利用。大川、山本等人[68]提出了采用扰动观测器或者模型参考前馈的方式来抑制机台振动,但这些方法控制器结构和算法复杂,不利于位置伺服周期的缩短。
采用传统的PID控制器设计方法以及控制器参数调整规则,精密工作台的运动控制精度和运动过程的振动抑制难于有效地同步实现,往往达不到期望的性能。为此,本文提出一种基于精密工作台振动模型,采用极点配置、模型参数匹配的方法设计PID控制器,实现对机台机械共振的抑制。
1 精密工作台机台振动模型
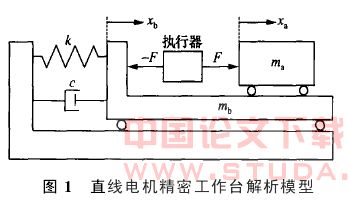
本文所涉及的直线电机精密运动工作台的机械模型,可以用一个如图1所示的惯性解析模型来表示,包括直线电机的定平台、动子、滑块等。根据图1所示解析模型,可以建立式(1)、(2)所示的精密工作台动力学方程:
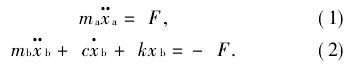
其中:ma是直线电机精密工作台的运动部分的质量,包括动子和工作台滑块的质量;F是直线电机的驱动力;xa是直线电机工作台的滑块相对于地基的绝对位移;mb是定平台的质量,包括直线电机定子和精密工作台机台质量;xb是定平台位移;k和c分别是定平台和地基在运动方向的连接刚度和连接阻尼。
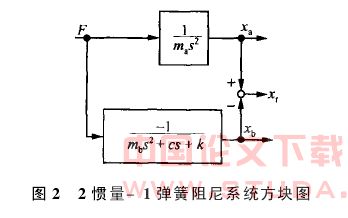
根据图1、式(1)以及式(2)可以得到图2所示的由动平台和定平台组成的2惯量-1弹簧阻尼系统方块图。图2中,xr是动平台相对定平台的位移。
根据图2、式(1)以及式(2)可以得到精密工作台系统从直线电机推力到动平台相对定平台的位移xr的传递函数为
考虑到定平台振动时控制对象模型的特征参数较多,采用传统的特征参数法来确定PID控制器的各项增益值时,选取的往往是有限的特征参数,难于同时满足运动控制精度和运动过程的振动抑制。
2 精密工作台运动控制器设计
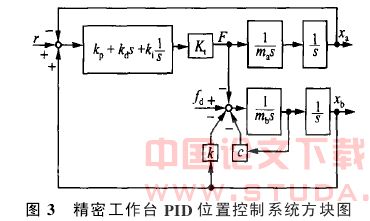
为了抑制精密工作台运动过程的振动,采用如图3所示的PID反馈控制,图3中的PID控制器基于部分模型匹配方法来设计[5,9]。
将式(3)表示的控制对象模型和直线电机电流放大环节组合并进行换算,使之具有分母系列表现形式[7],得到:
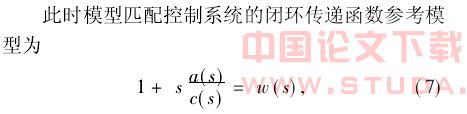
式中:w(s)是控制系统参考模型;a(s)是控制对象;c(s)是PID控制器的分子项,其中包含控制器待定参数。
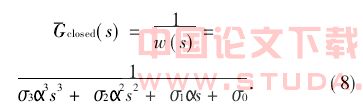
式中:σ0、σ1、σ2和σ3为闭环控制系统的标准传递函数系数;α为控制系统自由设计参数,通过α值的不同来平衡控制系统对指令响应和扰动抑制。根据模型跟踪控制的ITAE规则,推荐闭环控制系统的标准传递函数系数(σ0,σ1,σ2,σ3)=(1,1,0.5,0.15)。根据式(7)和式(8)可得PID控制器的参数数值表达式为:
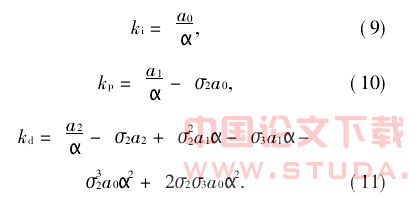
在式(9)—式(11)中,当控制对象模型和参考模型确定后,参数a0、a1、a2、σ2均可获得,而α为控制系统自由设计参数,表征闭环控制系统的时间常数。当α>0.0015时,控制系统闭环频率特性产生低频谐振,当α减小时,闭环系统谐振逐渐减小,而且闭环控制带宽也得到提高,系统相位滞后量减小。由此可知,在α<0.0015,所设计的PID控制器具有较好的定平台振动抑制效果。但如果α太小,PID控制系统的闭环控制带宽增加较快,一方面会将测量噪声引入到系统,影响系统的稳定性,另一方面,闭环控制带宽还要受采样频率的限制,因此α的选取要综合考虑。
3 控制系统的实验研究
系统实验的工作台及控制器参数如表1所示,取α=0.00075,可获得PID控制的表达式为
kPID(s)=2.46×105s2 3.212×107s 1.341×109/s. (12)
运动控制卡为具有开放伺服算法的Turbo-PMAC1,16位D/A输出,运动控制卡的采样周期和D/A刷新周期T为110μs。直线电机反馈光栅分辨率为0.1μm。利用PMAC的数据采集功能,采集光栅数据,然后利用Matlab得到如图4、5、6所示的实验结果。
图4为利用本文所提方法设计的控制器,1μm阶跃响应的仿真曲线和实测曲线。可以看出,系统的上升时间、超调量、建立时间与仿真结果都比较接近,系统有较好的动态响应特性。
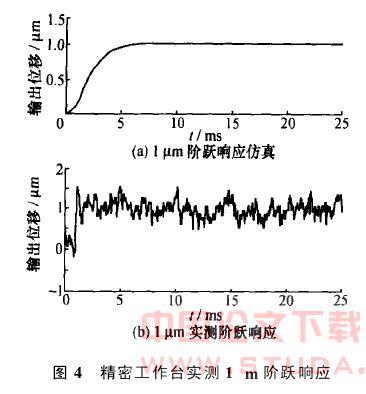图5是精密工作台以120mm/s匀速运动时两种控制方式的轨迹跟踪误差曲线。采用PID AF控制方式时,工作台跟踪误差平均值为1μm,跟踪误差波动范围为5μm;采用本文设计的PID控制器,轨迹跟踪误差平均值为0.5μm,跟踪误差波动范围为2μm。
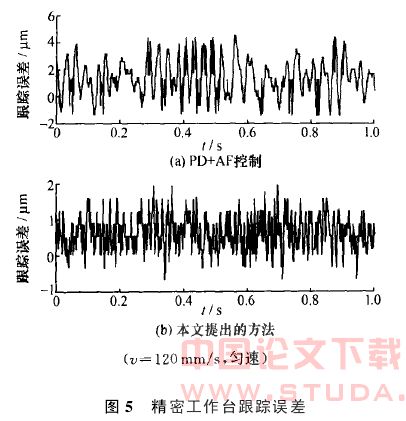
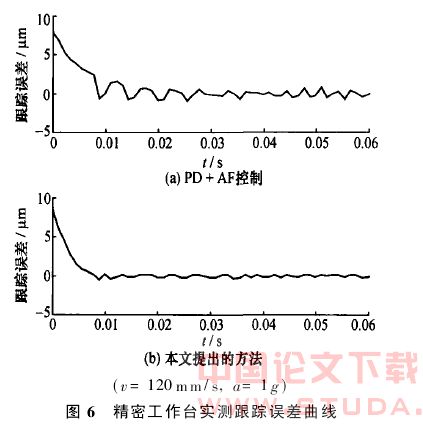
图6是精密工作台以速度120mm/s、加速度1g、运动距离240mm,在减速到停止过程中,两种控制方式在运动终点的轨迹跟踪误差曲线。采用PID AF控制方式时,运动结束有振荡,振荡幅值±2.5μm,工作台定位建立时间为25ms,采用本文设计的PID控制器,运动结束没有振荡,工作台定位建立时间为15ms。
由图5、图6可以看出,采用本文方法设计的PID控制器,精密工作台的定位精度、轨迹跟踪精度和定位建立时间都得到了提高。
4 结 论
仿真和实验表明,采用本文提出的基于振动模型的PID控制器设计方法,不但可以显著提高精密工作台定位精度、轨迹跟踪精度和定位建立时间,而且具有结构简单,计算量小的优点。论文成果已经在IC装备基础研究中得到应用,有较好的工程应用价值。
参考文献 (References)
[1]OTSUKAJio,HAYAMASadaji,OHASHIYasuji.Presentandfuturetechnologiesofprecisionandutraprecision
positioning[J].JournaloftheJapanSocietyofPrecisionEngineering,2001,67(2):173178.(inJapanese)
[2]HORIUCHIOsamu.Speedupofprecision/utraprecisionpositioning[J].JournaloftheJapanSocietyofPrecisionEngineering,2001,67(2):179183.(inJapanese)
[3]WAKUIShinji.Currentandfutureofprecisionstageworkinginstepper[J].JournaloftheJapanSocietyofPrecisionEngineering,2001,67(2):202206.(inJapanese)
[4]HASHIZUMEHitoshi,SHINNOHidenori.Developmentofhighspeednanometerpositioningtablesystemanditsper
ormancesevaluation[J].NipponKikaiGakkaiRonbunshu,CHen/TransactionsoftheJapanSocietyofMechanicalEngineers,PartC,
1998,64(626)C:411416.(inJapanese)
[5]WAKUIShinji.AstudyonPIDtuningofstagepositioningcontrolsystem[J].JournaloftheJapanSocietyofPrecisionEngineering,1999,65(5):763767.(inJapanese)
[6]WAKUIShinji,HOSHIMasashi,AKATSUKan.ApplicationofKitamori'smethodtostagepositioningcontro
lusingopenlooptransferfunction[J].NipponKikaiGakkaiRonbunshu,CHen/TransactionsoftheJapanSocietyofMechanicalEngineers,
PartC,2004,70(696)C:5562.(inJapanese)
[7]OHKAWAFujio,HOHDAHideki,KOBAYASHIJsuh,etal.Robustmodelfollowingcontrolofafeeddriver
systemhinderedbyamachinestandvibration[J].NipponKikaiGakkaiRonbunshu,CHen/TransactionsoftheJapanSocietyofMechanicalEngineers,PartC,
2002,68(668)C:101106.(inJapanese)
[8]YAMAMOTOAkiro,MIYAGAWAHidekazu,HAMATSUHiroshi.High-speedpositioningcontrolforlinearmotordrivingtablewithoutbasevibration[J].JournaloftheJapanSocietyofPrecisionEngineering,2004,70(5):645650.(inJapanese)
[9]WAKUIShinji.ApplicationofKitamori'smethodtostagepositioningcontrolsystem[J].NipponKikaiGakkaiRonbunshu,CHen/TransactionsoftheJapanSocietyofMechanicalEngineers,PartC,
1999,65(636)C:220227.(inJapanese)
原文网址：http://www.pipcn.com/research/200807/8965.htm
也许您还喜欢阅读：