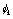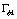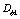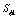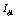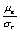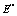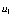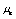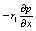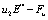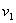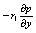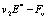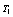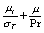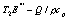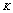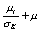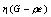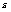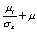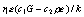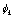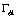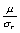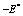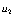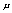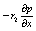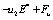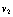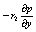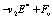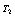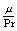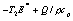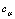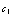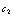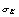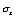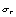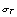立式陈列柜风幕数值模拟的双流体模型

• 改进的隧道监测系统(TMS)在隧道围岩变形监测中的应用
• 我国岩土工程在可持续发展中的新使命及其实现问题
• 矿山地质环境治理问题研究
• 岩土工程勘察中常见的技术问题及解决措施探讨
• RTK-GPS在广州新电视塔变形监测中的应用研究
• 既有建筑物加固修缮勘察与地基基础加固方案选择
• 现场测量建筑围护结构节能特性的问题分析
• 文物保护建筑勘察特点及工程实例分析
• 旁侧荷载对复合地基性状的影响
• 从工程实例分析谈顺层岩质边坡的勘察与参数选取

• 2013年中国建筑业前三季度分析简报
• 我对工程监理行业若干问题的思考
• 大学与建筑
• 从日本直岛的建设过程联想中国当代建筑发展
• 建筑服务业发展现状及营改增税制设计研究
• 椰子废弃物资源综合利用问题与对策
• 建筑生命周期环境管理与信息化解决方案
• 东莞至惠州城际铁路隧道安全风险评估与管理
• 工程爆破行业的信息化发展现状、实施问题和建议
• 改进的隧道监测系统(TMS)在隧道围岩变形监测中的应用

内容提示：考虑到陈列柜风幕的流动特点，采用双流体模型对立式陈列柜风幕进行数值模拟，其中内外风幕采用传统的K—紊流模型，陈列柜外的环境空气采用非紊流模型。两种流体之间的质量、动量和能量交换采用经验关系式处理。通过对风幕温度的测试结果比较发现，双流体模型的模拟结果相当吻合，是很有价值的的风幕计算模型。同时指出了双流体模型的不足和需要改进的地方。

延伸阅读：双流体模型 紊流 陈列柜 风幕

    余克志 丁国良 陈天及

    摘要：考虑到陈列柜风幕的流动特点，采用双流体模型对立式陈列柜风幕进行数值模拟，其中内外风幕采用传统的K—紊流模型，陈列柜外的环境空气采用非紊流模型。两种流体之间的质量、动量和能量交换采用经验关系式处理。通过对风幕温度的测试结果比较发现，双流体模型的模拟结果相当吻合，是很有价值的的风幕计算模型。同时指出了双流体模型的不足和需要改进的地方。
   
    关键词：陈列柜 风幕 双流体模型 紊流
   
   
   

    风幕对陈列柜的保温性能有十分重大的影响，国内外许多研究者对其进行过研究[1—8]。考虑到陈列柜的开口处的边界条件难于确定，为计算方便起见，很多研究者将开口处计算区域加以扩充，并认为扩充区域的边界不受陈列柜风幕的影响，其速度按无滑移的边界条件考虑，温度按实际测试的结果确定。由于陈列柜外由于风幕卷吸的环境空气流速很小，不会象风幕一样处于强烈的紊流状态。但他们的计算模型往往采用单一的紊流模型（K—e 模型，雷诺应力模型或者大涡模拟），这显然与实际情况不符。（参考《建筑中文网》）

    考虑到陈列柜外环境空气的非紊流特点，采用双流体模型对陈列柜风幕进行数值模拟，其中内外风幕采用传统的K—e紊流模型，陈列柜外的环境空气采用非紊流模型，同时考虑到两种流体之间的质量、动量和能量交换。

    紊流的双流体模型是Spalding提出的，其基本思路是：认为紊流流动可以看作两种流体各自的运动及其相互作用的综合；两种流体在时空上共存，具有各自的容积分数；两种流体认为是可以互相渗透的连续介质，它们的运动遵守各自的控制微分方程组；两种流体之间可能存在着质量、动量和能量方面的相互作用。两种流体的划分标准可以是流体的浓度、温度、流向等[9]。本文中以紊流和非紊流流体作为两种流体的划分标准。

    双流体模型应用于自由射流、羽流、壁面流和管流中取得了很大的成功，模拟结果和实际测试结果符合得很好[9-14]，但目前没有应用于陈列柜风幕的实例。从物理机理上分析，相对于紊流的单流体模型，双流体模型更能够准确地反应紊流的流动状况。但由于同时求解两套方程组，同时两种流体的方程之间存在强烈的耦和关系，其求解的难度更大，需要一定的求解技巧。

    2.1 控制方程

    风幕双流体模型的通用方程是[13]：

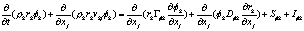
    (Ⅰ) (Ⅱ) (Ⅲ) (Ⅳ) (Ⅴ) (Ⅵ)

    其中下标k表示流体种类，可取为1或2，为方便起见，流体1表示紊流流体，流体2表示非紊流流体；下标j表示空间坐标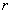；表示该种流体占有的体积分数（或存在几率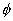）；表示因变量，取为1时对应连续性方程，如取速度、温度分别对应动量方程、能量方程。

    方程中的第(Ⅰ)项是不稳态项；第(Ⅱ)项是对流项；第(Ⅲ)项是扩散项；第(Ⅳ)项是相扩散项；第(Ⅴ)项是该流体内部的源项；第(Ⅵ)项是两种流体相互作用的源项。

    由于紊流流体采用K—e紊流模型，可得到紊流流体和非紊流流体的控制方程组[10,13-14]，如表1、2所示。

    表1 紊流流体的控制方程组

    表2 非紊流流体的控制方程组

    上两表中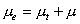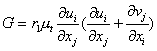，，，其余常数如下表3所示。

    表3 双流体模型的常数表

    2.2 两流体的质量、动量和能量交换关系

    双流体模型成功的关键在于两种流体的质量、动量和能量交换关系，从简单实用的角度出发，本文采用范维澄推荐的经验关系式[13]:

    2.2.1 质量交换

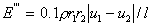    ，其中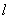为混合长度，下同。

    2.2.2 动量交换

    ；

    。

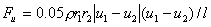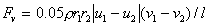    2.2.3 能量交换

    。

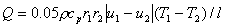    2.3 边界条件的设置

    2.3.1 风幕出风口

    分别取内外风幕速度、温度为测定值，其紊流容积分数。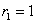

    2.3.2 环境空气

    取温度为环境温度设定值，相对压力取为0，其非紊流容积分数。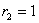

    2.3.3 风幕回风口

    取背压为-4Pa。

    2.3.4 壁面

    对紊流流体采用壁面函数法（wall function）

    2.4 混合物参量计算

    采用双流体模型分别计算出两种流体的参数分布后，可以采用时间平均来计算各状态参量的平均分布。

    任一参量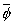（速度、温度等）与两流体对应值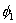和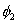的关系式是：

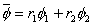
    3.1 容积分数

   
    图1 紊流流体容积分数

    图1是紊流流体容积分数分布图，从图上可以看出，紊流区域主要集中在陈列柜内部，在陈列柜外侧有少量溢出，而陈列柜外的广大计算区域完全处于非紊流状态。这说明采用双流体模型计算陈列柜风幕是符合物理机理的。

    3.2 速度场

   
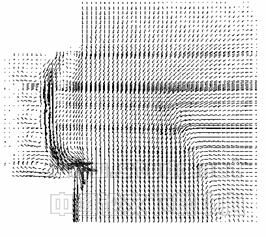
    图2 陈列柜速度场

    图2是陈列柜速度场分布图。可以看出，由于风幕的卷吸作用，外界环境的热空气有向陈列柜流动的迹象，这也是陈列柜热负荷的主要来源；而风幕流出的冷空气也在回风口附近溢出陈列柜外，造成了陈列柜冷量的损失，这是陈列柜设计时需要加以考虑的地方。

    3.3 温度场

   
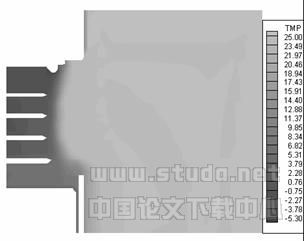
    图3 陈列柜温度场

    图3是陈列柜温度场分布图。可以看出，陈列柜外的热空气的温度基本稳定在环境温度左右（25℃）。而由于风幕的遮挡作用，陈列柜内温度依然较低。从陈列柜内到柜外，其温度有很大的升高，特别是风幕流经的地方，温度梯度极大。

    为了考察双流体模型用于陈列柜风幕的可行性，特取实际测试的三层搁架外侧的温度场与计算模拟值进行对比分析。其结果如图4～6所示。

   
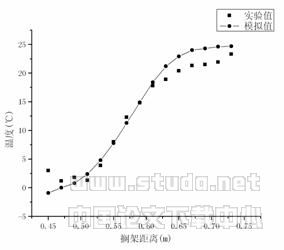
    图4 第一层搁架外层温度模拟值与实验值比较

   
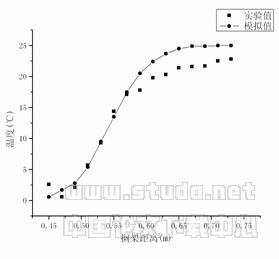
    图5 第二层搁架外层温度模拟值与实验值比较

   
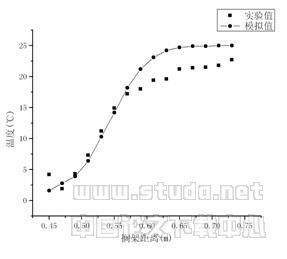
    图6 第三层搁架外层温度模拟值与实验值比较

    图4～6表明，双流体模型的模拟结果与实际测试结果温度值是比较符合的，特别是在风幕流动区域内（图中0.5m～0.66m之间），两者之间符合得非常好。

    在搁架外侧，计算模拟值存在普遍偏高的现象，除了考虑试验测试值受测试环境风速的影响外，有两个因素必须加以考虑：一是双流体模型所依赖的K—e 模型在考虑非紊流流体下的修正问题。按照Malin的观点，需要在K方程和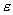方程的源项中各加上一项“附加源项”，否则紊流的扩散会被低估[10]；二是在计算两种流体的质量转换时，只考虑流体2（非紊流流体）转化为流体1（紊流流体），而没有考虑流体1（紊流流体）转化为流体2（非紊流流体）。因此需要对前述的质量交换关系式进行修正[13]。

    本文采用双流体模型对立式陈列柜的风幕进行了数值模拟，其模拟结果与实验测试结果比较吻合，说明双流体模型是陈列柜风幕模拟的一种有价值的模型。同时指出了双流体模型在陈列柜风幕数值模拟上存在的不足，提出了其改进的方向。

    [1] 余克志, 丁国良, 陈天及. 立式陈列柜空气流动与热湿交换的整体模型[J]. 上海交通大学学报, 2005, 39(2): 220-224.

    [2] 穆景阳, 陈江平, 娄骏, 等. 卧式超市陈列柜风幕系统数值分析[J]. 工程热物理学报, 2001, 22(3): 313-315.

    [3] 刘东毓, 吴业正, 程松. 陈列柜内空气流动与换热的研究[J]. 制冷学报, 2000, (1): 51-55.

原文网址：http://www.pipcn.com/research/200601/8404.htm

也许您还喜欢阅读：